题目内容
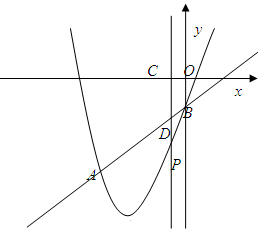
如图,抛物线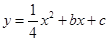 与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线
与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线 于点C;
于点C;
(1)求该抛物线的解析式;
(2)求点A关于直线 的对称点
的对称点 的坐标,判定点
的坐标,判定点 是否在抛物线上,并说明理由;
是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段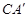 于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
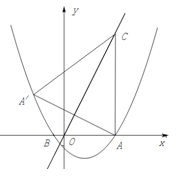
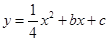 与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线
与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线 于点C;
于点C;(1)求该抛物线的解析式;
(2)求点A关于直线
 的对称点
的对称点 的坐标,判定点
的坐标,判定点 是否在抛物线上,并说明理由;
是否在抛物线上,并说明理由;(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段
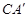 于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)抛物线的解析式为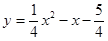 .
.
(2)点A/的坐标为(﹣3,4),点A/在该抛物线上,理由见解析.
(3)存在,当点P运动到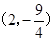 时,四边形PACM是平行四边形.理由见解析.
时,四边形PACM是平行四边形.理由见解析.
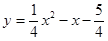 .
.(2)点A/的坐标为(﹣3,4),点A/在该抛物线上,理由见解析.
(3)存在,当点P运动到
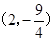 时,四边形PACM是平行四边形.理由见解析.
时,四边形PACM是平行四边形.理由见解析.试题分析:(1)把A(5,0)、B(-1,0)两点代入二次函数解析式
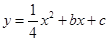 中,解方程组得到b、c的值,即可求得抛物线的解析式.
中,解方程组得到b、c的值,即可求得抛物线的解析式.(2)过点
 作
作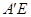 ⊥x轴于E,AA/与OC交于点D,可证得
⊥x轴于E,AA/与OC交于点D,可证得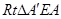 ∽
∽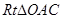 ;再由相似三角形对应边成比例,可以求得点A′的坐标.然后把点A的坐标代入抛物线的解析式
;再由相似三角形对应边成比例,可以求得点A′的坐标.然后把点A的坐标代入抛物线的解析式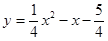 ,验证点A′是否在抛物线上即可.
,验证点A′是否在抛物线上即可.(3)存在.设直线
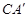 的解析式为y=kx+b,将点C和点A′的坐标代入直线方程,即可得到直线
的解析式为y=kx+b,将点C和点A′的坐标代入直线方程,即可得到直线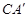 的解析式为
的解析式为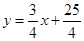 ;设点P的坐标为
;设点P的坐标为 ,则点M为
,则点M为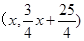 ,要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,则有
,要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,则有 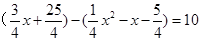 ,解此方程即可得到
,解此方程即可得到点P的坐标.
试题解析:(1)∵
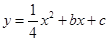 与x轴交于A(5,0)、B(-1,0)两点,
与x轴交于A(5,0)、B(-1,0)两点,∴
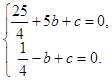 , 解得
, 解得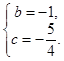
∴抛物线的解析式为
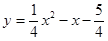 .························································3分
.························································3分(2)过点
 作
作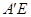 ⊥x轴于E,AA/与OC交于点D,
⊥x轴于E,AA/与OC交于点D,∵点C在直线y=2x上, ∴C(5,10)
∵点A和
 关于直线y=2x对称,
关于直线y=2x对称,∴OC⊥
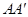 ,
,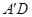 =AD.
=AD.∵OA=5,AC=10,
∴
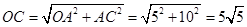 .
.∵
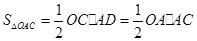 , ∴
, ∴ .∴
.∴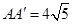 .·············5分
.·············5分在
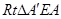 和Rt
和Rt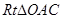 中,
中,∵∠
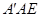 +∠
+∠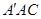 =90°,∠ACD+∠
=90°,∠ACD+∠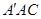 =90°,
=90°, ∴∠
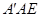 =∠ACD.
=∠ACD.又∵∠
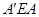 =∠OAC=90°,
=∠OAC=90°,∴
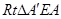 ∽
∽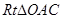 .
.∴
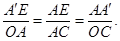 即
即 .
.∴
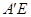 =4,AE=8.
=4,AE=8.∴OE=AE-OA=3.
∴点A/的坐标为(﹣3,4).·······························7分
当x=﹣3时,
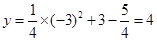 .
.所以,点A/在该抛物线上.································8分

存在.
理由:设直线
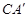 的解析式为y=kx+b,
的解析式为y=kx+b,则
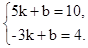 ,解得
,解得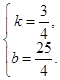
∴直线
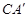 的解析式为
的解析式为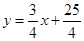 .··················9分
.··················9分设点P的坐标为
 ,则点M为
,则点M为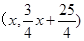 .
.∵PM∥AC,
∴要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,
∴
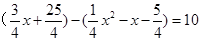 .
.解得
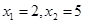 (不合题意,舍去)当x=2时,
(不合题意,舍去)当x=2时,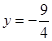 .
.∴当点P运动到
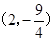 时,四边形PACM是平行四边形.····················11分
时,四边形PACM是平行四边形.····················11分
练习册系列答案
相关题目
 位于第二象限的图象上,点B1,B2,…,B2011在函数
位于第二象限的图象上,点B1,B2,…,B2011在函数 、
、 ,…,
,…, 都是正方形,则正方形
都是正方形,则正方形

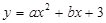 经过
经过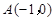 、
、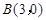 、C三点,点
、C三点,点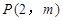 是抛物线与直线
是抛物线与直线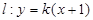 的一个交点.
的一个交点.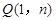 ,求
,求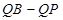 的最大值;
的最大值;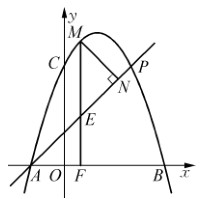
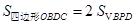 ;
;
 (m是常数)
(m是常数)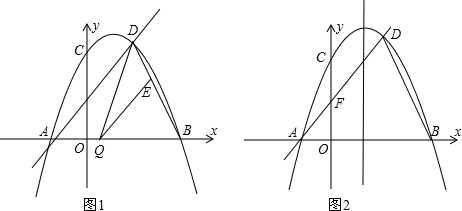
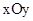 中,抛物线
中,抛物线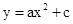 与x轴交于点A(-2,0)和点B,与y轴交于点C(0,
与x轴交于点A(-2,0)和点B,与y轴交于点C(0,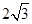 ),线段AC上有一动点P从点A出发,以每秒1个单位长度的速度向点C移动,线段AB上有另一个动点Q从点B出发,以每秒2个单位长度的速度向点A移动,两动点同时出发,设运动时间为t秒.
),线段AC上有一动点P从点A出发,以每秒1个单位长度的速度向点C移动,线段AB上有另一个动点Q从点B出发,以每秒2个单位长度的速度向点A移动,两动点同时出发,设运动时间为t秒.

