题目内容
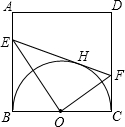
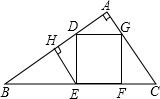 已知:如图,正方形DEFG内接入Rt△ABC,EF在斜边BC上,EH⊥AB于H.
已知:如图,正方形DEFG内接入Rt△ABC,EF在斜边BC上,EH⊥AB于H.
求证:(1)△ADG≌△HED;(2)EF2=BE•FC.
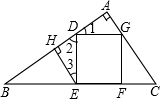 证明:(1)∵DEFG为正方形,
证明:(1)∵DEFG为正方形,∴∠EDG=90°,
∴∠1+∠2=90°.
∵EH⊥AB,
∴∠2+∠3=90°,
∴∠1=∠3.
又∠A=∠EHD=90°,DG=DE,
∴△ADG≌△HED.
(2)在Rt△ABC中,∠B+∠C=90°.
在Rt△BDE中,∠B+∠2=90°.
∴∠2=∠C.
∴Rt△BDE∽Rt△GCF,
∴DE:FC=BE:GF.
又∵DE=GF=EF,
∴

分析:(1)根据题意,∠A=∠DHE=90°,DG=DE,根据“AAS”只需再证一对角相等即可.
因为∠ADG+∠HDE=90°,∠HDE+∠HED=90°,
所以∠ADG=∠HED.
(2)欲证结论,即证EF:BE=FC:EF.根据正方形边长相等,转证DE:BE=FC:FG,即证明△BDE∽△GFC.
点评:此题考查了直角三角形相似的判定和性质,难度中等.证明题常运用分析法寻找突破口.

练习册系列答案
相关题目
 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.



 于E,交CD于F.
于E,交CD于F.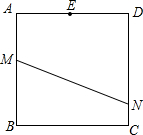 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.