题目内容
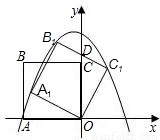
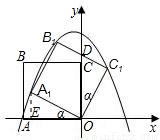
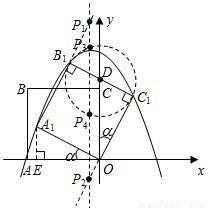
如图,正方形ABCO的边长为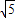 ,以O为原点建立平面直角坐标系,点A在x轴的负半轴上,点C在y轴的正半轴上,把正方形ABCO绕点O顺时针旋转α后得到正方形A1B1C1O(α<45°),B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.
,以O为原点建立平面直角坐标系,点A在x轴的负半轴上,点C在y轴的正半轴上,把正方形ABCO绕点O顺时针旋转α后得到正方形A1B1C1O(α<45°),B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.(1)求tanα的值;
(2)求点A1的坐标,并直接写出点B1、点C1的坐标;
(3)求抛物线的函数表达式及其对称轴;
(4)在抛物线的对称轴上是否存在点P,使△PB1C1为直角三角形?若存在,直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
【答案】分析:(1)根据旋转的知识可知:四边形A1B1C1O为正方形,∴OC1=B1C1,∠OC1B1=90°,∠C1OD=∠AOA1=α,又∵D是B1C1的中点,∴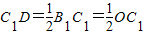 ,∴在Rt△C1OD中,tanα=
,∴在Rt△C1OD中,tanα=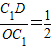 .∴tanα的值是
.∴tanα的值是 ;
;
(2)根据三角函数与勾股定理即可求得点A1的坐标,并直接写出点B1、点C1的坐标;要注意方程思想的应用;
(3)将点A1,B1,C1的坐标代入解析式,利用方程组即可求得解析式,再求得对称轴;
(4)一种是与线段B1C1垂直的直线:分别过点B1、C1;一种是根据直径所对的圆周角是直角求得,以线段B1C1为直径作圆,与对称轴的交点即是所求点.
解答:解:(1)∵四边形A1B1C1O为正方形,
∴OC1=B1C1,∠OC1B1=90度.
又∵D是B1C1的中点,
∴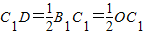 .
.
∵由旋转性质可知,∠C1OD=∠AOA1=α,
∴在Rt△C1OD中,tanα=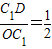 .
.
∴tanα的值是 .(2分)
.(2分)
(2)过点A1作A1E⊥x轴,垂足为点E.
在Rt△A1EO中,tanα=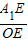 ,
,
∴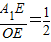 .
.
设A1E=k,则OE=2k,在Rt△A1EO中,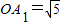 ,
,
根据勾股定理,得A1E2+OE2=OA12.
即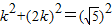 ,
,
解得k1=-1(舍),k2=1.
∴A1E=1,OE=2.
又∵点A1在第二象限,
∴点A1的坐标为(-2,1).(4分)
直接写出点B1的坐标为(-1,3),点C1的坐标为(1,2).(6分)
(3)∵抛物线y=ax2+bx+c过点A1,B1,C1.
∴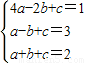
解得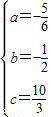
∴抛物线的函数表达式为 .(8分)
.(8分)
将其配方,得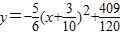 .
.
∴抛物线的对称轴是直线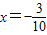 .(9分)
.(9分)
(4)存在点P,使△PB1C1为直角三角形.(10分)
满足条件的点P共有4个: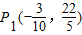 ,
,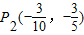 ,
,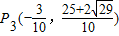 ,
,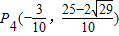 .(14分)
.(14分)
点评:此题属于中考中的压轴题,难度较大,知识点考查的较多而且联系密切,需要学生认真审题.此题考查了二次函数与一次函数,三角形、四边形的综合知识,解题的关键是要注意数形结合思想的应用.
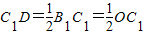 ,∴在Rt△C1OD中,tanα=
,∴在Rt△C1OD中,tanα=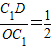 .∴tanα的值是
.∴tanα的值是 ;
;(2)根据三角函数与勾股定理即可求得点A1的坐标,并直接写出点B1、点C1的坐标;要注意方程思想的应用;
(3)将点A1,B1,C1的坐标代入解析式,利用方程组即可求得解析式,再求得对称轴;
(4)一种是与线段B1C1垂直的直线:分别过点B1、C1;一种是根据直径所对的圆周角是直角求得,以线段B1C1为直径作圆,与对称轴的交点即是所求点.
解答:解:(1)∵四边形A1B1C1O为正方形,
∴OC1=B1C1,∠OC1B1=90度.
又∵D是B1C1的中点,
∴
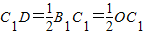 .
.∵由旋转性质可知,∠C1OD=∠AOA1=α,
∴在Rt△C1OD中,tanα=
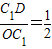 .
.∴tanα的值是
 .(2分)
.(2分)(2)过点A1作A1E⊥x轴,垂足为点E.
在Rt△A1EO中,tanα=
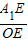 ,
,
∴
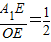 .
.设A1E=k,则OE=2k,在Rt△A1EO中,
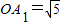 ,
,根据勾股定理,得A1E2+OE2=OA12.
即
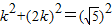 ,
,解得k1=-1(舍),k2=1.
∴A1E=1,OE=2.
又∵点A1在第二象限,
∴点A1的坐标为(-2,1).(4分)
直接写出点B1的坐标为(-1,3),点C1的坐标为(1,2).(6分)
(3)∵抛物线y=ax2+bx+c过点A1,B1,C1.
∴
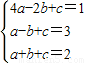
解得
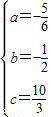

∴抛物线的函数表达式为
 .(8分)
.(8分)将其配方,得
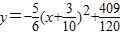 .
.∴抛物线的对称轴是直线
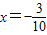 .(9分)
.(9分)(4)存在点P,使△PB1C1为直角三角形.(10分)
满足条件的点P共有4个:
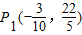 ,
,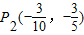 ,
,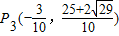 ,
,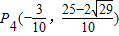 .(14分)
.(14分)点评:此题属于中考中的压轴题,难度较大,知识点考查的较多而且联系密切,需要学生认真审题.此题考查了二次函数与一次函数,三角形、四边形的综合知识,解题的关键是要注意数形结合思想的应用.

练习册系列答案
相关题目
 如图,正方形ABCO放在平面直角坐标系中,其中点O为坐标原点,A、C两点分别在x轴的负半轴和y轴的正半轴上,点B的坐标为(-4,4).已知点E、点F分别从A、点B同时出发,点E以每秒2个单位长度的速度在线段AB上来回运动.点F沿B→C→0方向,以每秒1个单位长度的速度向点O运动,当点F到达点O时,E、F两点都停止运动.在E、F的运动过程中,存在某个时刻,使得△OEF的面积为6.那么点E的坐标为
如图,正方形ABCO放在平面直角坐标系中,其中点O为坐标原点,A、C两点分别在x轴的负半轴和y轴的正半轴上,点B的坐标为(-4,4).已知点E、点F分别从A、点B同时出发,点E以每秒2个单位长度的速度在线段AB上来回运动.点F沿B→C→0方向,以每秒1个单位长度的速度向点O运动,当点F到达点O时,E、F两点都停止运动.在E、F的运动过程中,存在某个时刻,使得△OEF的面积为6.那么点E的坐标为 如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1.
如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1. 如图,正方形ABCO的边长是2,E是BC中点,则E点的坐标是
如图,正方形ABCO的边长是2,E是BC中点,则E点的坐标是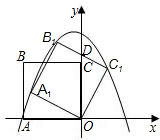 B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.
B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.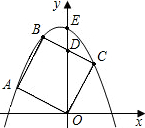 x2+bx+c经过B、C且与y轴的交点为
x2+bx+c经过B、C且与y轴的交点为