题目内容
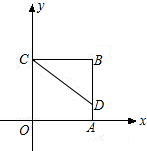
 如图,正方形ABCO放在平面直角坐标系中,其中点O为坐标原点,A、C两点分别在x轴的负半轴和y轴的正半轴上,点B的坐标为(-4,4).已知点E、点F分别从A、点B同时出发,点E以每秒2个单位长度的速度在线段AB上来回运动.点F沿B→C→0方向,以每秒1个单位长度的速度向点O运动,当点F到达点O时,E、F两点都停止运动.在E、F的运动过程中,存在某个时刻,使得△OEF的面积为6.那么点E的坐标为
如图,正方形ABCO放在平面直角坐标系中,其中点O为坐标原点,A、C两点分别在x轴的负半轴和y轴的正半轴上,点B的坐标为(-4,4).已知点E、点F分别从A、点B同时出发,点E以每秒2个单位长度的速度在线段AB上来回运动.点F沿B→C→0方向,以每秒1个单位长度的速度向点O运动,当点F到达点O时,E、F两点都停止运动.在E、F的运动过程中,存在某个时刻,使得△OEF的面积为6.那么点E的坐标为分析:由于点E、F同时运动,根据它们位置的不同,可分成三种情况进行讨论:0<t≤2,2<t≤4,4<t<8.
解答:解:设时间为t秒
①当0<t≤2时,AE=2t,BE=4-2t,BF=t,FC=4-t,CD=4,
s△OEF=s正方形OABC-S△AEO-S△BEF-S△OCF=16-4t-2(4-t)-t(2-t)=t2-4t+8,
∵s△OEF=6,即t2-4t+8=6,解得t=2+
或t=2-
,又∵0<t≤2,∴t=2-
.
此时,点E的坐标为(-4,4-2
);
②当2<t≤4时,AE=8-2t,BE=2t-4,BF=t,FC=4-t,CD=4,
s△OEF=s正方形OABC-S△AEO-S△BEF-S△OCF=16-4(4-t)-2(4-t)-t(t-2)=-t2+8t-8,
∵s△OEF=6,即-t2+8t-8=6,解得t=4+
或t=4-
,又∵2<t≤4,∴t=4-
.
此时,点E的坐标为(-4,2
);
③当4<t<8时,AE=2t-8,FC=t-4,OF=8-t,
s△OEF=
×4×(8-t)=16-2t,
∵s△OEF=6,即16-2t=6,解得t=5,此时,点E的坐标为(-4,2);
故点E的坐标为(-4,4-2
),(-4,2
),(-4,2).
①当0<t≤2时,AE=2t,BE=4-2t,BF=t,FC=4-t,CD=4,
s△OEF=s正方形OABC-S△AEO-S△BEF-S△OCF=16-4t-2(4-t)-t(2-t)=t2-4t+8,
∵s△OEF=6,即t2-4t+8=6,解得t=2+
| 2 |
| 2 |
| 2 |
此时,点E的坐标为(-4,4-2
| 2 |
②当2<t≤4时,AE=8-2t,BE=2t-4,BF=t,FC=4-t,CD=4,
s△OEF=s正方形OABC-S△AEO-S△BEF-S△OCF=16-4(4-t)-2(4-t)-t(t-2)=-t2+8t-8,
∵s△OEF=6,即-t2+8t-8=6,解得t=4+
| 2 |
| 2 |
| 2 |
此时,点E的坐标为(-4,2
| 2 |
③当4<t<8时,AE=2t-8,FC=t-4,OF=8-t,
s△OEF=
| 1 |
| 2 |
∵s△OEF=6,即16-2t=6,解得t=5,此时,点E的坐标为(-4,2);
故点E的坐标为(-4,4-2
| 2 |
| 2 |
点评:解答本题要充分利用正方形的特殊性质.注意在正方形中的特殊三角形的应用,会用运动时间表示边长,面积,搞清楚正方形中的三角形的三边关系等,可有助于提高解题速度和准确率.

练习册系列答案
相关题目
 如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1.
如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1. 如图,正方形ABCO的边长是2,E是BC中点,则E点的坐标是
如图,正方形ABCO的边长是2,E是BC中点,则E点的坐标是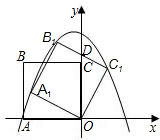 B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.
B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.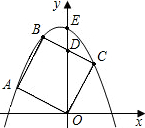 x2+bx+c经过B、C且与y轴的交点为
x2+bx+c经过B、C且与y轴的交点为