题目内容
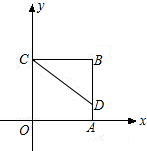 如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1.
如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1.(1)直接写出点D1的坐标;
(2)求点D旋转到点D1所经过的路线长.
分析:(1)把△CBD顺时针旋转90°,得到△CB1D1.如图所示,B1D1=BD=3,D1在x轴负半轴上,所以D1(-3,0).
(2)路线是以C为圆心,CD为半径,圆心角为90°的扇形的弧.根据弧长公式求解.
(2)路线是以C为圆心,CD为半径,圆心角为90°的扇形的弧.根据弧长公式求解.
解答: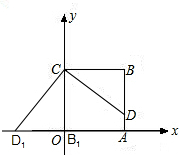 解:(1)D1(-3,0). (2分)
解:(1)D1(-3,0). (2分)
(2)∵正方形ABCO的边长为4,D为AB上一点,且BD=3,
根据勾股定理可求得CD=5. (3分)
∴点D旋转到点D1
所经过的路线长为
×2π×5=
π. (5分)
 解:(1)D1(-3,0). (2分)
解:(1)D1(-3,0). (2分)(2)∵正方形ABCO的边长为4,D为AB上一点,且BD=3,
根据勾股定理可求得CD=5. (3分)
∴点D旋转到点D1
所经过的路线长为
| 1 |
| 4 |
| 5 |
| 2 |
点评:旋转前后对应线段相等.注意根据点所在位置确定点的坐标.此题还考查了弧长公式的运用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图,正方形ABCO放在平面直角坐标系中,其中点O为坐标原点,A、C两点分别在x轴的负半轴和y轴的正半轴上,点B的坐标为(-4,4).已知点E、点F分别从A、点B同时出发,点E以每秒2个单位长度的速度在线段AB上来回运动.点F沿B→C→0方向,以每秒1个单位长度的速度向点O运动,当点F到达点O时,E、F两点都停止运动.在E、F的运动过程中,存在某个时刻,使得△OEF的面积为6.那么点E的坐标为
如图,正方形ABCO放在平面直角坐标系中,其中点O为坐标原点,A、C两点分别在x轴的负半轴和y轴的正半轴上,点B的坐标为(-4,4).已知点E、点F分别从A、点B同时出发,点E以每秒2个单位长度的速度在线段AB上来回运动.点F沿B→C→0方向,以每秒1个单位长度的速度向点O运动,当点F到达点O时,E、F两点都停止运动.在E、F的运动过程中,存在某个时刻,使得△OEF的面积为6.那么点E的坐标为 如图,正方形ABCO的边长是2,E是BC中点,则E点的坐标是
如图,正方形ABCO的边长是2,E是BC中点,则E点的坐标是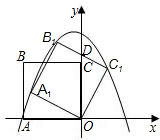 B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.
B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1. x2+bx+c经过B、C且与y轴的交点为
x2+bx+c经过B、C且与y轴的交点为