Question

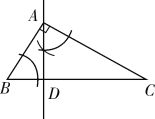
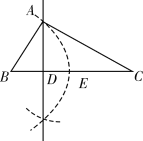
【题目】（1）如图1，已知，平分外角，平分外角．直接写出和的数量关系，不必证明；

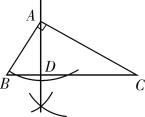
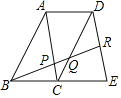
（2）如图2，已知，和三等分外角，和三等分外角．试确定和的数量关系，并证明你的猜想；（不写证明依据）

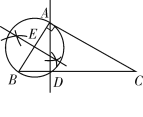
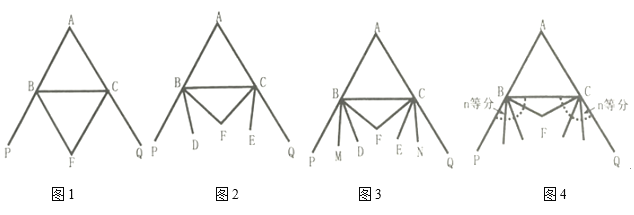
（3）如图3，已知，、和四等分外角，、和四等分外角．试确定和的数量关系，并证明你的猜想；（不写证明依据）

（4）如图4，已知，将外角进行分，是临近边的等分线，将外角进行等分，是临近边的等分线，请直接写出和的数量关系，不必证明．

Answer 1

【答案】（1）；（2）；（3）；（4）．

【解析】

（1）由平分外角，平分外角，结合三角形外角的性质与三角形内角和定理，即可得到结论；

（2）由和三等分外角，和三等分外角，结合三角形外角的性质与三角形内角和定理，即可得到结论；

（3）由、和四等分外角，、和四等分外角，结合三角形外角的性质与三角形内角和定理，即可得到结论；

（4）由外角进行分，是临近边的等分线，将外角进行等分，是临近边的等分线，合三角形外角的性质与三角形内角和定理，即可得到结论；

（1），理由如下：

∵平分外角，平分外角，

∴，，

∵，，

∴，

∴；

（2），理由如下：

由已知得：，，

∵，，

∴，

；

（3），理由如下：

由已知得：，，

∵，，

∴，

，

（4），理由如下：

由已知得：，，

∵，，

∴，

∴．