题目内容
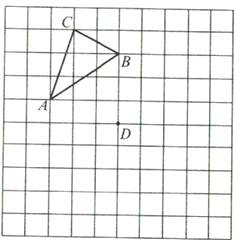
【题目】如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，连结BF，CE．下列说法①△BDF≌△CDE；②△ABD和△ACD面积相等；③BF∥CE；④CE=BF．其中正确的有（ ）
A.1个B.2个C.3个D.4个
【答案】D
【解析】
根据三角形的中线把一个三角形分成两个面积相等的三角形可判断②；利用SAS可证△BDF≌△CDE；根据全等三角形的性质可知∠ECD=∠FBD，CE=BF，根据平行线的判定定理可得BF∥CE.
∵AD是△ABC的中线
∴BD=CD，△ABD和△ACD面积相等，故②正确；
∵DE=DF，∠BDF=∠CDE
∴△BDF≌△CDE（SAS），故①正确；
∴∠ECD=∠FBD，CE=BF，故④正确；
∴BF∥CE，故③正确；
正确的有①②③④，共4个
故选D
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
【题目】课外阅读是提高学生综合素养的重要途径，某校为了解学生课外阅读情况，随机抽取若干名学生，调查他们平均每天课外阅读的时间（
小时），并将收集的数据绘制成如图所示的两幅不完整的统计图表，请根据图表信息，解答下列问题：
某校学生平均每天课外阅读时间频数表
类别 | 时间 | 频数（人） | 频率 |
A |
| 10 |
|
B |
| 20 | 0．4 |
C |
| 15 | 0．3 |
D |
|
|
|
某校学生平均每天课外阅读时间条形统计图
（1）填空：
________，
________；并在图中补全条形统计图；
（2）该校现有学生1200人，请你根据上述调查结果，估计该校学生平均每天课外阅读时间不少于1小时的共有多少人？
