��Ŀ����
����Ŀ���Ķ����в��ϲ�������⣺
����֪��![]() �ļ�������������������
�ļ�������������������![]() ��Ӧ�ĵ���ԭ��ľ��룺
��Ӧ�ĵ���ԭ��ľ��룺 ![]() ��Ҳ����˵��
��Ҳ����˵�� ![]() ��ʾ����������
��ʾ����������![]() ����0��Ӧ��֮��ľ��룻
����0��Ӧ��֮��ľ��룻
������ۿ����ƹ�Ϊ![]() ��ʾ����������
��ʾ����������![]() ����
����![]() ��Ӧ�ĵ�֮��ľ��룻
��Ӧ�ĵ�֮��ľ��룻
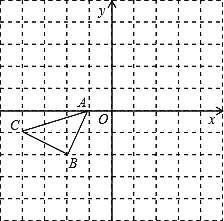
��1�ⷽ��![]() ��������������������ԭ�����Ϊ2�ĵ��Ӧ����Ϊ
��������������������ԭ�����Ϊ2�ĵ��Ӧ����Ϊ![]() �����÷��̵Ľ�Ϊ
�����÷��̵Ľ�Ϊ![]() ��
��
��2�ⲻ��ʽ![]() ����ͼ�����������ҳ�
����ͼ�����������ҳ�![]() �Ľ⣬����1�ľ���Ϊ2�ĵ��Ӧ����Ϊ
�Ľ⣬����1�ľ���Ϊ2�ĵ��Ӧ����Ϊ![]() ��3����
��3����![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ��
��![]() .
.

��3�ⷽ��![]() �ɾ���ֵ�ļ�������֪���÷��̱�ʾ������������1��
�ɾ���ֵ�ļ�������֪���÷��̱�ʾ������������1��![]() �ľ���֮��Ϊ5�Ķ�Ӧ��
�ľ���֮��Ϊ5�Ķ�Ӧ��![]() ��ֵ.�������ϣ�1��
��ֵ.�������ϣ�1��![]() �ľ���Ϊ3�����㷽�̵�
�ľ���Ϊ3�����㷽�̵�![]() ��Ӧ�ĵ���1���ұ�
��Ӧ�ĵ���1���ұ�![]() ����ߣ���
����ߣ���![]() ��Ӧ�ĵ���1���ұߣ�����ͼ���Կ���
��Ӧ�ĵ���1���ұߣ�����ͼ���Կ���![]() ��ͬ������
��ͬ������![]() ��Ӧ�ĵ���
��Ӧ�ĵ���![]() ����ߣ��ɵ�
����ߣ��ɵ�![]() ����ԭ���̵Ľ���
����ԭ���̵Ľ���![]() ��
��![]() .
.
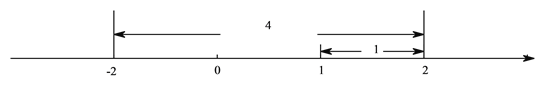
�ش����⣺��ֻ��ֱ��д���𰸣�
�ٽⷽ��![]()
�ڽⲻ��ʽ![]()
�۽ⷽ��![]()
���𰸡���1�� x=1��x=-7;��2��x��7����x��-1;��3��x=![]() ��x=
��x=![]() .
.
���������������: �ٸ������������÷���حx+3|=4�Ľ⣻
�ڸ������������ò���ʽ|x-3|��4�ý⼯��
������x�IJ�ͬȡֵ��Χ������÷���|x-3|+|x+2|=8�Ľ⣮
�������:
�ٽⷽ��|x+3|=4��������������������3����Ϊ4�ĵ�Ķ�Ӧ��Ϊ7��1�����÷��̵Ľ�Ϊx=7��x=1��
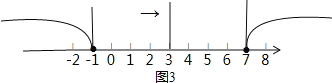
�ڽⲻ��ʽ|x3|4��
��ͼ3�����������ҳ�|x3|=4�Ľ⣬����3�ľ���Ϊ4�ĵ��Ӧ����Ϊ1��7����|x3|>4�Ľ⼯Ϊx1��x7.
��|x3|+|x+2|=8��
��x<2ʱ��
3xx2=8��
��ã�x=3.5��
��x=2ʱ��
|22|+|2+2|=4��8��
��x=2����ʹ��|x3|+|x+2|=8������
��2<x3ʱ��
3x+x+2=5��8��
��2<x3ʱ������ʹ��|x3|+|x+2|=8������
��x>3ʱ��
x3+x+2=8��
��ã�x=4.5����
��|x3|+|x+2|=8�Ľ���x=3.5��x=4.5.
�㾦:���⿼���˺�����ֵ���ŵ�һԪһ�η��̣�Ū���Ķ������еķ��������÷�������˼���ǽⱾ��Ĺؼ�.

 ����ѧҵ���Ե�����ϵ�д�
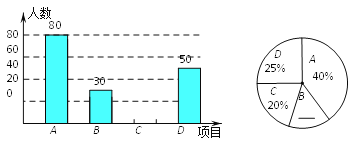
����ѧҵ���Ե�����ϵ�д�����Ŀ����һ�������ĺ�����װ��ֻ����ɫ��ͬ�ĺڡ���������40����Сӱ������ʵ�飬�����������������Ⱥ�����������һ���������ɫ���ٰ����Żغ����У������ظ��������̣��±���ʵ���е�һ��ͳ�����ݣ�
����Ĵ��� | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
��������Ĵ��� | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
���������Ƶ�� | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
��1������ƣ���![]() �ܴ�ʱ�����������Ƶ�ʽ���ӽ� ������ȷ��0.1��
�ܴ�ʱ�����������Ƶ�ʽ���ӽ� ������ȷ��0.1��
��2����������һ�Σ�����������ĸ���P������= ��
��3���Թ��������ڡ���������ɫ������ж���ֻ��