题目内容
【题目】如图①,正方形![]() 的边长为
的边长为![]() ,动点
,动点![]() 从点
从点![]() 出发,在正方形的边上沿
出发,在正方形的边上沿![]() 运动,设运动的时间为
运动,设运动的时间为![]() ,点
,点![]() 移动的路程为
移动的路程为![]() ,
,![]() 与
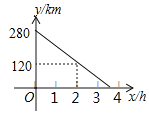
与![]() 的函数图象如图②,请回答下列问题:
的函数图象如图②,请回答下列问题:

(1)点![]() 在
在![]() 上运动的时间为
上运动的时间为 ![]() ,在
,在![]() 上运动的速度为
上运动的速度为 ![]()
(2)设![]() 的面积为
的面积为![]() ,求当点
,求当点![]() 在
在![]() 上运动时,
上运动时,![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
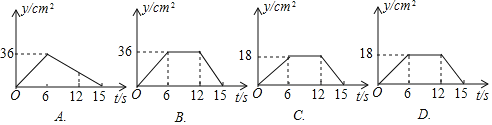
(3)①下列图表示![]() 的面积
的面积![]() 与时间
与时间![]() 之间的函数图象是 .
之间的函数图象是 .
②当![]()
![]() 时,
时,![]() 的面积为
的面积为![]()
【答案】(1)6,2;(2)![]() ;(3)①C;②4或13.
;(3)①C;②4或13.
【解析】
(1)由图象得:点P在AB上运动的时间为6s,在CD上运动的速度为6÷(15-12)=2(cm/s);
(2)当点P在CD上运动时,由题意得:PC=2(t-12),得出PD=30-2t,由三角形面积公式即可得出答案;
(3)①当点P在AB上运动时,y与t之间的函数解析式为y=3t;当点P在BC上运动时,y与t之间的函数解析式为y=18;当点P在CD上运动时,y与t之间的函数解析式为y=-6t+90,即可得出答案;
②由题意分两种情况,即可得出结果.
(1)由题意得:点![]() 在
在![]() 上运动的时间为
上运动的时间为![]() ,
,
在![]() 上运动的速度为
上运动的速度为![]() ;
;
故答案为:6,2;
(2)当点![]() 在
在![]() 上运动时,
上运动时,
由题意得:![]() ,
,
![]() ,
,
![]() 的面积为
的面积为![]() ,
,
即![]() 与
与![]() 之间的函数解析式为
之间的函数解析式为![]() ;
;
(3)①当点![]() 在
在![]() 上运动时,
上运动时,![]() 与
与![]() 之间的函数解析式为
之间的函数解析式为![]() ;
;
当点![]() 在
在![]() 上运动时,
上运动时,![]() 与
与![]() 之间的函数解析式为
之间的函数解析式为![]() ;
;
当点![]() 在
在![]() 上运动时,
上运动时,![]() 与
与![]() 之间的函数解析式为
之间的函数解析式为![]() ,
,
![]() 表示
表示![]() 的面积
的面积![]() 与时间
与时间![]() 之间的函数图象是
之间的函数图象是![]() ,
,
故答案为:![]() ;
;
②由题意得:当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
即当![]() 或
或![]() 时,
时,![]() 的面积为
的面积为![]() ;
;
故答案为:4或13.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目