题目内容
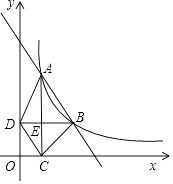
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC=4.点P是△ABC内的一点,连接PC,以PC为直角边在PC的右上方作等腰直角三角形PCD.连接AD,若AD∥BC,且四边形ABCD的面积为12,则BP的长为 . 
【答案】![]()
【解析】解:如图,作PF⊥BC于点F,延长FP交AD于点E, 
∵AD∥BC,
∴∠PFC=∠DEP=90°,
∴∠CPF+∠PCF=90°,
∵∠DPC=90°,
∴∠CPF+∠DPE=90°,
∴∠PCF=∠DPE,
在△PCF和△DPE中,
∵  ,
,
∴△PCF≌△DPE(AAS),
∴PF=DE、PE=CF,
设PF=DE=x,则PE=CF=4﹣x,
∵S四边形ABCD= ![]() (AD+BC)AB=12,
(AD+BC)AB=12,
∴ ![]() ×(AD+4)×4=12,解得AD=2,
×(AD+4)×4=12,解得AD=2,
∴AE=BF=2﹣x,
∴FC=BC﹣BF=4﹣(2﹣x)=2+x,
可得2+x=4﹣x,解得x=1,
∴BP= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】掌握等腰直角三角形是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
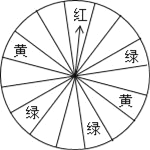
【题目】“六一”儿童节期间,某商厦为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准哪个区域,顾客就可以获得相应的奖品.
颜色 | 奖品 |
红色 | 玩具熊 |
黄色 | 童话书 |
绿色 | 彩笔 |
小明和妈妈购买了125元的商品,请你分析计算:
(1)小明获得奖品的概率是多少?
(2)小明获得童话书的概率是多少?