题目内容
【题目】如图,在平面直角坐标系中,函数y= ![]() (x>0,k是常数)的图象经过A(2,6),B(m,n),其中m>2.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连结AD,DC,CB.
(x>0,k是常数)的图象经过A(2,6),B(m,n),其中m>2.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连结AD,DC,CB.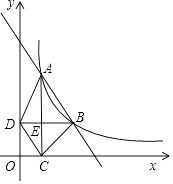
(1)若△ABD的面积为3,求k的值和直线AB的解析式;
(2)求证: ![]() =
= ![]() ;
;
(3)若AD∥BC,求点B的坐标.
【答案】
(1)
解:∵函数y= ![]() (x>0,k是常数)的图象经过A(2,6),
(x>0,k是常数)的图象经过A(2,6),
∴k=2×6=12,
∵B(m,n),其中m>2.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,
∴mn=12①,BD=m,AE=6﹣n,
∵△ABD的面积为3,
∴ ![]() BDAE=3,
BDAE=3,
∴ ![]() m(6﹣n)=3②,
m(6﹣n)=3②,
联立①②得,m=3,n=4,
∴B(3,4);
设直线AB的解析式为y=kx+b(k≠0),
则 ![]() ,
,
∴ ![]() ,
,
∴直线AB的解析式为y=﹣2x+10
(2)
证明:∵A(2,6),B(m,n),
∴BE=m﹣2,CE=n,DE=2,AE=6﹣n,
∴DEAE=2(6﹣n)=12﹣2n,
BECE=n(m﹣2)=mn﹣2n=12﹣2n,
∴DEAE=BECE,
∴ ![]()
(3)
解:由(2)知, ![]() ,
,
∵∠AEB=∠DEC=90°,
∴△DEC∽△BEA,
∴∠CDE=∠ABE
∴AB∥CD,
∵AD∥BC,
∴四边形ADCB是平行四边形.
又∵AC⊥BD,
∴四边形ADCB是菱形,
∴DE=BE,CE=AE.
∴B(4,3)
【解析】(1)先求出k的值,进而得出mn=12,然后利用三角形的面积公式建立方程,联立方程组求解即可;(2)先表示出BE,CE,DE,AE,进而求出BECE和DECE即可得出结论;(3)利用(2)的结论得出△DEC∽△BEA,进而得出AB∥CD,即可得出四边形ADCB是菱形即可得出点B的坐标.

 阅读快车系列答案
阅读快车系列答案【题目】小明到某服装专卖店去做社会调查,了解到该专卖店为了微励营业员的工作积极性,实行“月总收入=基本工资(固定)+计付奖金”的方法计算薪资,并获得如下信息;
营业员 | 小张 | 小王 |
月销售件数 | 200 | 150 |
月总收入/元 | 1400 | 1250 |
销售每件奖励a元,晋业员月基本工资为b元.
(1)列方程组求a,b的值.
(2)假设月销售件数为x,月总收入为y元,请写出y与x的函数关系式,并求出营业员小张上个月总收入是1700元时,小张上个月卖了多少件服装?
【题目】有这样一个问题:
计算代数式![]() (其中x≠0)的值后填入下表.并根据表格所反映出的
(其中x≠0)的值后填入下表.并根据表格所反映出的![]() (其中x≠0)的值与x之间的变化规律进行探究.
(其中x≠0)的值与x之间的变化规律进行探究.
x | …… | 0.25 | 0.5 | 1 | 10 | 100 | 1000 | 10000 | …… |
| …… | …… |
下面是小东计算代数式![]() (其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:
(其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:
x | …… | 0.25 | 0.5 | 1 | 10 | 100 | 1000 | 10000 | …… |
| …… | 2 | 1 |
|
|
|
| …… |
(1)上表是![]() (其中x≠0)与x的几组对应值.直接写出x=10时,求代数式
(其中x≠0)与x的几组对应值.直接写出x=10时,求代数式![]() 的值;
的值;
(2)随着x值的增大,代数式![]() 的值有何变化(回答“增大”或“减少”);
的值有何变化(回答“增大”或“减少”);
(3)当x值无限增大时,代数式![]() 的值无限趋近于一个数,这个数是多少.
的值无限趋近于一个数,这个数是多少.