题目内容
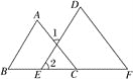
【题目】如图,已知Rt△ABD中,∠A=90°,将斜边BD绕点B顺时针方向旋转至BC,使BC∥AD,过点C作CE⊥BD于点E. 
(1)求证:△ABD≌△ECB;
(2)若∠ABD=30°,BE=3,求弧CD的长.
【答案】
(1)证明:∵∠A=90°,CE⊥BD,
∴∠A=∠BEC=90°.
∵BC∥AD,
∴∠ADB=∠EBC.
∵将斜边BD绕点B顺时针方向旋转至BC,
∴BD=BC.
在△ABD和△ECB中,

∴△ABD≌△ECB
(2)解:∵△ABD≌△ECB,
∴AD=BE=3.
∵∠A=90°,∠BAD=30°,
∴BD=2AD=6,
∵BC∥AD,
∴∠A+∠ABC=180°,
∴∠ABC=90°,
∴∠DBC=60°,
∴弧CD的长为 ![]() =2π
=2π
【解析】(1)因为这两个三角形是直角三角形,根据旋转的性质得出BC=BD,由AD∥BC推出∠ADB=∠EBC,从而能证明△ABD≌△ECB;(2)由全等三角形的性质得出AD=BE=3.根据30°角所对的直角边等于斜边的一半得出BD=2AD=6,根据平行线的性质求出∠DBC=60°,再代入弧长计算公式求解即可.
【考点精析】根据题目的已知条件,利用弧长计算公式和旋转的性质的相关知识可以得到问题的答案,需要掌握若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

【题目】有这样一个问题:
计算代数式![]() (其中x≠0)的值后填入下表.并根据表格所反映出的
(其中x≠0)的值后填入下表.并根据表格所反映出的![]() (其中x≠0)的值与x之间的变化规律进行探究.
(其中x≠0)的值与x之间的变化规律进行探究.
x | …… | 0.25 | 0.5 | 1 | 10 | 100 | 1000 | 10000 | …… |
| …… | …… |
下面是小东计算代数式![]() (其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:
(其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:
x | …… | 0.25 | 0.5 | 1 | 10 | 100 | 1000 | 10000 | …… |
| …… | 2 | 1 |
|
|
|
| …… |
(1)上表是![]() (其中x≠0)与x的几组对应值.直接写出x=10时,求代数式
(其中x≠0)与x的几组对应值.直接写出x=10时,求代数式![]() 的值;
的值;
(2)随着x值的增大,代数式![]() 的值有何变化(回答“增大”或“减少”);
的值有何变化(回答“增大”或“减少”);
(3)当x值无限增大时,代数式![]() 的值无限趋近于一个数,这个数是多少.
的值无限趋近于一个数,这个数是多少.