��Ŀ����
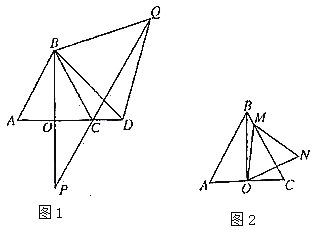
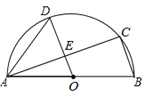
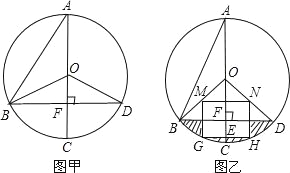
����Ŀ����ͼ�ף���֪�ڡ�O�У�AB=![]() ��AC�ǡ�O��ֱ����AC��BD��F����A=30�ȣ�
��AC�ǡ�O��ֱ����AC��BD��F����A=30�ȣ�
��1������BC��CD�������ж��ı���OBCD�Ǻ���������ı��Σ���˵�����ɣ�
��2����������OBDΧ��һ��Բ���棬��������Բ�ĵ���Բ�İ뾶��
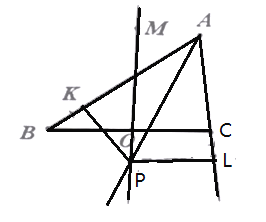
��3����ͼ�ң���������A=30�㡱��Ϊ����A=22.5�㡱�������������䣬�뾶OB��OD���е�M��NΪ����������MNGH������G��H�ڡ�O���ӻ�![]() �ϣ�GH��OC�ڵ�E������ͼ����Ӱ���ֵ����������������У�
�ϣ�GH��OC�ڵ�E������ͼ����Ӱ���ֵ����������������У�
���𰸡���1���ı���OBCD��������֤������������2��![]() ����3��
����3��![]() ��
��
��������
��1�����ݶԽ����ഹֱ��ƽ���ı��������ν���֤������AC��BD�����ݴ���������֪��BF=FD����ֻ��֤��OF=CF����Rt��ABF�У���֪��A��AB���ɽ�BF��AF�ij��������Rt��BOF�У����ù��ɶ����ɽ��뾶OB��OF���������CF=2OB-AF�ɽ�CF���������OF=CF��BF=FD��BD��OC����֤�ı���OBCDΪ���Σ�
��2����֪����BOD��Բ�ĽǺͰ뾶������l����=![]() ������⣬�ٸ��ݵ����ܳ���2��r=l�����������Բ����İ뾶��
������⣬�ٸ��ݵ����ܳ���2��r=l�����������Բ����İ뾶��
��3���������ߣ�����OH��S��Ӱ=S����OBD-S��BOD-S�¾�����S����=![]() lR��S��BOD=
lR��S��BOD=![]() OB2���������ݿɽ�����AOB�͡�BOD������������M��N�ǡ�OBD����λ�ߣ���֪MN=
OB2���������ݿɽ�����AOB�͡�BOD������������M��N�ǡ�OBD����λ�ߣ���֪MN=![]() BD����Rt��OEH�У����ݹ��ɶ��������OE����OF=
BD����Rt��OEH�У����ݹ��ɶ��������OE����OF=![]() OB���ɵ�EF=OE-OF���ʣ�S�¾���=MN��EF���Ӷ��ɽ���Ӱ���ֵ���������
OB���ɵ�EF=OE-OF���ʣ�S�¾���=MN��EF���Ӷ��ɽ���Ӱ���ֵ���������
�⣺��1���ı���OBCD�����Σ�
��ͼ������AC��BD��AC��ֱ����
��AC��ֱƽ��BD��
��BF=FD��![]() ��
��
���BAD=2��BAC=60�㣬
���BOD=120�㣮
��BF=![]() AB=2
AB=2![]() ��
��
��Rt��ABF��
AF=![]() ,
,
��Rt��BOF��
��OB2=BF2+OF2����![]() ��
��
��ã�OB=4��
��OA=OB=4��
��OF=AF��AO=6��4=2��
��AC=2OA=8��
��CF=AC��AF=8��6=2��
��CF=OF��
��BF=FD��AC��BD��
���ı���OBCD�����Σ�
��2����Բ�ĵ���Բ�İ뾶Ϊr�����ܳ�Ϊ2��r��
������OBD�Ļ���=![]() ��
��
��![]() ��
��
��ã�r=![]() ��
��
��3����ͼ��������OH��
�ߡ�A=22.5�㣬
���BOC=45�㣬
�ߡ�BOD=��BOC=90��
��뾶OB=r���ɹ��ɶ�������![]()
�����r2=24��2��![]() ��
��
��M��N��OB��OD���е㣬
���ı���MNGH�Ǿ��Σ�
��MN2=GH2=12��2��![]() ����EH2=EG2=
����EH2=EG2=![]() MN2=3��2��
MN2=3��2��![]() ����
����
��Rt��HOE��OE2=OH2��HE2����OE2=r2��3��2��![]() ����
����
��ã�OE2=21��2��![]() ����
����
���¾��ε����=��OE��OF����MN=![]() ��
��
������OBD�����=![]() ��
��
��ͼ����Ӱ���ֵ����=![]() -
-![]()
=![]() ��
��

 ��ѧʵ����ϵ�д�
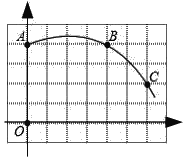
��ѧʵ����ϵ�д�����Ŀ��ij�мס��������������۹�˾��ȥ��һ��ʮ�·�ÿ������ͬ��Ʒ�������������ͼ��ʾ��
![]() ���������ͼ��д�±���
���������ͼ��д�±���
���۹�˾ | ƽ���� | ���� | ��λ�� | ���� |
�� |
| 9 | ||
�� | 9 |
| 8 |
![]() ���������������ͬ�ķ���Լס��������������۹�˾ȥ��һ��ʮ�·ݵ�����������з�����
���������������ͬ�ķ���Լס��������������۹�˾ȥ��һ��ʮ�·ݵ�����������з�����
![]() ��ƽ�����ͷ����Ͽ���
��ƽ�����ͷ����Ͽ���
![]() ������ͼ�ϼס��������������۹�˾�������������ƿ�
������ͼ�ϼס��������������۹�˾�������������ƿ�![]() �����ĸ��������۹�˾����DZ��
�����ĸ��������۹�˾����DZ��![]() ��
��