题目内容
已知正比例函数y=kx与反比例函数y=| a |
| x |
(1)求出a+k的值.
(2)当x为何值时,kx>
| a |
| x |
分析:(1)先根据题意可知A、B两点关于原点对称,即x=-1,y=2,把点A(1,2)分别代入正比例函数y=kx与反比例函数y=
.求得a,k的值,所以可得a+k=4;
(2)kx>
,即2x>
,解得不等式即可.
| a |
| x |
(2)kx>
| a |
| x |
| 2 |
| x |
解答:解:(1)因为反比例函数是中心对称图形,
所以A、B两点关于原点对称,
即x=-1,y=2,
把点A(1,2)分别代入正比例函数y=kx与反比例函数y=
,
得k=2,a=2,
所以a+k=4;
(2)kx>
,即2x>
,
解得x>1或-1<x<0,
故x>1或-1<x<0时,kx>
.
所以A、B两点关于原点对称,
即x=-1,y=2,
把点A(1,2)分别代入正比例函数y=kx与反比例函数y=
| a |
| x |
得k=2,a=2,
所以a+k=4;
(2)kx>
| a |
| x |
| 2 |
| x |
解得x>1或-1<x<0,
故x>1或-1<x<0时,kx>
| a |
| x |
点评:本题综合考查反比例函数与方程以及不等式的相关知识点.先由点的坐标求函数解析式,根据不等关系解x的范围,体现了数形结合的思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知正比例函数y=k1x(k1≠0)与反比例函数y=
(k2≠0)的图象有一个交点的坐标为(-2,-1),则它的另一个交点的坐标是( )
| k2 |
| x |
| A、(2,1) |
| B、(-2,-1) |
| C、(-2,1) |
| D、(2,-1) |
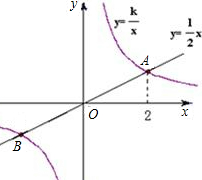 横坐标为2.
横坐标为2. 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3).