题目内容
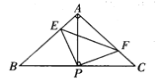
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F.给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③ 2S四边形AEPF=S△ABC;④EF=PC.上述结论正确的有 ( ).
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
证明△AEP≌△CFP,从而得到①,证明△APF≌△BPE,继而判定△EPF是等腰直角三角形,从而得到②,根据S四边形AEPF=S△AEP+S△APF,经过推导得出③,只有当EF是中位线时EF=CP才成立,从而判断④不一定正确,据此即可得答案.
∵在△ABC中,AB=AC,∠BAC=90°,P是BC中点,
∴AP=PC=PB,∠B=∠C=∠BAP=∠CAP=45°,AP⊥BC,
∴∠APB=∠APC=90°,
∵∠EPF=90°,
∴∠APE=∠CPF=90°-∠APF,
在△AEP和△CFP中,
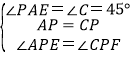 ,
,
∴△AEP≌△CFP,
同理△APF≌△BPE,
∴AE=CF,PE=PF,
∴△EPF是等腰直角三角形,
∴S△AEP=S△CPF,
∴S四边形AEPF=S△AEP+S△APF,
=S△CPF+S△APF,
=S△APC,
=![]() S△ABC,
S△ABC,
即2S四边形AEPF=S△ABC;
只有当EF为中位线时才有EF=CP,其余情况下都不相等,
∴①②③正确,④错误,
即正确的有3个,
故选C.

练习册系列答案
相关题目