题目内容
【题目】在△ABC中，∠ACB=90°，AC=BC=4，M为AB的中点．D是射线BC上一个动点，连接AD，将线段AD绕点A逆时针旋转90°得到线段AE，连接ED，N为ED的中点，连接AN，MN．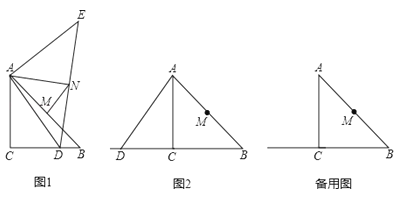 
（1）如图1，当BD=2时，AN等于多少？，NM与AB的位置关系是？
（2）当4＜BD＜8时，
①依题意补全图2；
②判断（1）中NM与AB的位置关系是否发生变化，并证明你的结论；
（3）连接ME，在点D运动的过程中，当BD的长为何值时，ME的长最小？最小值是多少？请直接写出结果．
【答案】解：（1）∵∠ACB=90°，AC=BC=4，BD=2，
∴CD=2，
∴AD=
=2
，
∵将线段AD绕点A逆时针旋转90°得到线段AE，
∴△ADE是等腰直角三角形，
∴DE=
AD=2
，
∵N为ED的中点，
∴AN=
DE=，
∵M为AB的中点，
∴AM=AB=2，
∵
，
∴
，
∵∠CAB=∠DAN=45°，
∴∠CAD=∠MAN，
∴△ACD∽△AMN，
∴∠AMN=∠C=90°，
∴MN⊥AB，
故答案为：，垂直；
（2）①补全图形如图2所示，
②（1）中NM与AB的位置关系不发生变化，
理由：∵∠ACB=90°，AC=BC，
∴∠CAB=∠B=45°，
∴∠CAN+∠NAM=45°，
∵线段AD绕点A逆时针旋转90°得到线段AE，
∴AD=AE，∠DAE=90°，
∵N为ED的中点，
∴
，AN⊥DE，
∴∠CAN+∠DAC=45°，
∴∠NAM=∠DAC，在Rt△AND中，
DAN=cos45°=
，
同理
=，
∴=
，
∵∠DAC=45°﹣∠CAN=∠MAN，
∴△ANM∽△ADC，
∴∠AMN=∠ACD，
∵D在BC的延长线上，
∴∠ACD=180°﹣∠ACB=90°，
∴∠AMN=90°，
∴MN⊥AB；
（3）连接ME，EB，过M作MG⊥EB于G，过A作AK⊥AB交BD的延长线于K，
则△AKB等腰直角三角形，
在△ADK与△ABE中，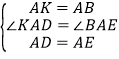
，
∴△ADK≌△ABE，
∴∠ABE=∠K=45°，
∴△BMG是等腰直角三角形，
∵BC=4，
∴AB=4，MB=2，
∴MG=2，
∵∠G=90°，
∴ME≥MG，
∴当ME=MG时，ME的值最小，
∴ME=BE=2，
∴DK=BE=2，
∵CK=BC=4，
∴CD=2，
∴BD=6，
∴BD的长为6时，ME的长最小，最小值是2．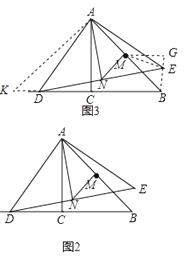
【解析】（1）根据已知条件得到CD=2，根据勾股定理得到AD==2 ， 根据旋转的性质得到△ADE是等腰直角三角形，求得DE=AD=2 ， 根据直角三角形的性质得到AN=DE= ， AM=AB=2 ， 推出△ACD∽△AMN，根据相似三角形的性质即可得到结论；
（2）①根据题意补全图形即可；②根据等腰直角三角形的性质得到∠CAB=∠B=45°，求得∠CAN+∠NAM=45°根据旋转的性质得到AD=AE，∠DAE=90°，推出△ANM△ADC，由相似三角形的性质得到∠AMN=∠ACD，即可得到结论；
（3）连接ME，EB，过M作MG⊥EB于G，过A作AK⊥AB交BD的延长线于K，得到△AKB等腰直角三角形，推出△ADK≌△ABE，根据全等三角形的性质得到∠ABE=∠K=45°，证得△BMG是等腰直角三角形，求出BC=4，AB=4 ， MB=2 ， 由ME≥MG，于是得到当ME=MG时，ME的值最小，根据等量代换即可得到结论．
【考点精析】关于本题考查的等腰直角三角形和勾股定理的概念，需要了解等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案．
