Question

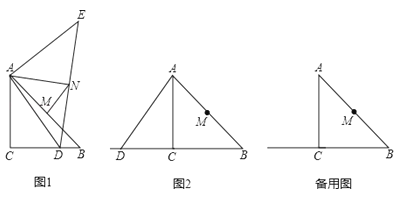
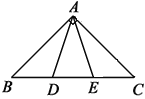
【题目】如图，在△ABC中， ∠BAC=90°， AB=AC=2，点D，E均在边BC上，且∠DAE=45°，若BD=1，则DE=__________．

Answer 1

【答案】

【解析】分析：根据等腰直角三角形的性质得把△ABD绕点A逆时针旋转得到△ACF,连接如图，根据旋转的性质得 接着证明然后根据“SAS”可判断△ADE≌△AFE，得到DE=FE，由于根据勾股定理得设 则 则由此即可解决问题．

详解：

∴

把△ABD绕点A逆时针旋转得到△ACF,连接 如图,则

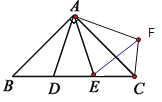
△ABD≌△ACF,

∵

∴

∴

即

∴∠EAD=∠EAF，

在△ADE和△AFE中

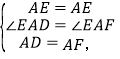
∴△ADE≌△AFE，

∴DE=FE，

∵

∴

Rt△ABC中，∵

∴

∵

设 则

则有

解得：

∴

故答案为：