题目内容
【题目】在初中数学学习阶段,我们常常会利用一些变形技巧来简化式子,解答问题.
材料一:在解决某些分式问题时,倒数法是常用的变形技巧之一,所谓倒数法,即把式子变成其倒数形式,从而运用约分化简,以达到计算目的.
例:已知:![]() ,求代数式x2+
,求代数式x2+![]() 的值.
的值.
解:∵![]() ,∴
,∴![]() =4
=4
即![]() =4∴x+
=4∴x+![]() =4∴x2+
=4∴x2+![]() =(x+
=(x+![]() )2﹣2=16﹣2=14
)2﹣2=16﹣2=14
材料二:在解决某些连等式问题时,通常可以引入参数“k”,将连等式变成几个值为k的等式,这样就可以通过适当变形解决问题.
例:若2x=3y=4z,且xyz≠0,求![]() 的值.
的值.
解:令2x=3y=4z=k(k≠0)
则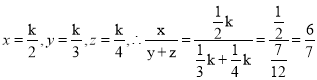
根据材料回答问题:
(1)已知![]() ,求x+
,求x+![]() 的值.
的值.
(2)已知![]() ,(abc≠0),求
,(abc≠0),求![]() 的值.
的值.
(3)若![]() ,x≠0,y≠0,z≠0,且abc=7,求xyz的值.
,x≠0,y≠0,z≠0,且abc=7,求xyz的值.
【答案】(1)5;
(2)![]() ;
;
(3)![]()
【解析】
(1)仿照材料一,取倒数,再约分,利用等式的性质求解即可;
(2)仿照材料二,设![]() =
=![]() =
=![]() =k(k≠0),则a=5k,b=2k,c=3k,代入所求式子即可;
=k(k≠0),则a=5k,b=2k,c=3k,代入所求式子即可;
(3)本题介绍两种解法:
解法一:(3)解法一:设![]() =
=![]() =
=![]() =
=![]() (k≠0),化简得:
(k≠0),化简得:![]() ①,
①,![]() ②,
②,![]() ③,相加变形可得x、y、z的代入
③,相加变形可得x、y、z的代入![]() =
=![]() 中,可得k的值,从而得结论;
中,可得k的值,从而得结论;
解法二:取倒数得:![]() =
=![]() =
=![]() ,拆项得
,拆项得![]() ,从而得x=
,从而得x=![]() ,z=
,z=![]() ,代入已知可得结论.
,代入已知可得结论.
解:(1)∵![]() =
=![]() ,
,
∴![]() =4,
=4,
∴x﹣1+![]() =4,
=4,
∴x+![]() =5;
=5;
(2)∵设![]() =
=![]() =
=![]() =k(k≠0),则a=5k,b=2k,c=3k,
=k(k≠0),则a=5k,b=2k,c=3k,
∴![]() =
=![]() =
=![]() =
=![]() ;
;
(3)解法一:设![]() =
=![]() =
=![]() =
=![]() (k≠0),
(k≠0),
∴![]() ①,
①,![]() ②,
②,![]() ③,
③,
①+②+③得:2(![]() )=3k,
)=3k,
![]() =
=![]() k④,
k④,
④﹣①得:![]() =
=![]() k,
k,
④﹣②得:![]() ,
,
④﹣③得:![]() k,
k,
∴x=![]() ,y=
,y=![]() ,z=
,z=![]() 代入
代入![]() =
=![]() 中,得:
中,得:
 =
=![]() ,
,
![]() ,
,
k=4,
∴x=![]() ,y=
,y=![]() ,z=
,z=![]() ,
,
∴xyz=![]() =
=![]() =
=![]() ;
;
解法二:∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
将其代入![]() 中得:
中得:  =
=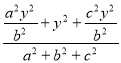
![]() =
=![]() ,y=
,y=![]() ,
,
∴x=![]() ,z=
,z=![]() =
=![]() ,
,
∴xyz=![]() =
=![]() .
.

练习册系列答案
相关题目