题目内容
【题目】已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣1，0），点C（0，5），另抛物线经过点（1，8），M为它的顶点．
（1）求抛物线的解析式；
（2）求△MCB的面积S△MCB ．
（3）在坐标轴上，是否存在点N，满足△BCN为直角三角形？如存在，请直接写出所有满足条件的点N．
【答案】
（1）
解：∵二次函数y=ax2+bx+c的图象经过A（﹣1，0），C（0，5），（1，8），
则有： 
，
解得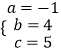 
．
∴抛物线的解析式为y=﹣x2+4x+5
（2）
解：令y=0，得（x﹣5）（x+1）=0，x1=5，x2=﹣1，
∴B（5，0）．
由y=﹣x2+4x+5=﹣（x﹣2）2+9，得顶点M（2，9）
如图1中，作ME⊥y轴于点E，
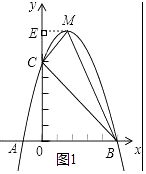
可得S△MCB=S梯形MEOB﹣S△MCE﹣S△OBC= 
（2+5）×9﹣ ×4×2﹣ ×5×5=15
（3）
解：存在．如图2中，
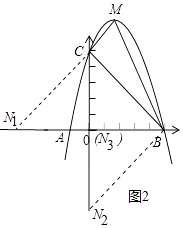
∵OC=OB=5，
∴△BOC是等腰直角三角形，
①当C为直角顶点时，N1（﹣5，0）．
②当B为直角顶点时，N2（0，﹣5）．
③当N为直角顶点时，N3（0，0）．
综上所述，满足条件的点N坐标为（0，0）或（0，﹣5）或（﹣5，0）
【解析】（1）把A（﹣1，0），C（0，5），（1，8）三点代入二次函数解析式，解方程组即可．（2）先求出M、B、C的坐标，根据S△MCB=S梯形MEOB﹣S△MCE﹣S△OBC即可解决问题．（3）分三种情①C为直角顶点；②B为直角顶点；③N为直角顶点；分别求解即可．
【考点精析】掌握二次函数的图象和二次函数的性质是解答本题的根本，需要知道二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
