Question

【题目】已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣1，0），点C（0，5），另抛物线经过点（1，8），M为它的顶点．

（1）求抛物线的解析式；
（2）求△MCB的面积S△MCB ．

Answer 1

【答案】
（1）

解：依题意： ，

解得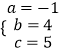

∴抛物线的解析式为y=﹣x2+4x+5

（2）

解：令y=0，得（x﹣5）（x+1）=0，x1=5，x2=﹣1，

∴B（5，0）．

由y=﹣x2+4x+5=﹣（x﹣2）2+9，得M（2，9）

作ME⊥y轴于点E，

可得S△MCB=S梯形MEOB﹣S△MCE﹣S△OBC= （2+5）×9﹣ ×4×2﹣ ×5×5=15．

【解析】（1）将已知的三点坐标代入抛物线中，即可求得抛物线的解析式．（2）可根据抛物线的解析式先求出M和B的坐标，由于三角形MCB的面积无法直接求出，可将其化为其他图形面积的和差来解．过M作ME⊥y轴，三角形MCB的面积可通过梯形MEOB的面积减去三角形MCE的面积减去三角形OBC的面积求得．
【考点精析】通过灵活运用二次函数的图象和二次函数的性质，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小即可以解答此题．