题目内容
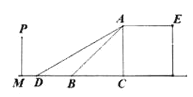
【题目】如图,为美化中心城区环境,政府计划在长为30米,宽为20米的矩形场地![]() 上修建公园.其中要留出宽度相等的三条小路,且两条与
上修建公园.其中要留出宽度相等的三条小路,且两条与![]() 平行,另一条与
平行,另一条与![]() 平行,其余部分建成花圃.
平行,其余部分建成花圃.
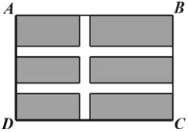
(1)若花圃总面积为448平方米,求小路宽为多少米?
(2)已知某园林公司修建小路的造价![]() (元)和修建花圃的造价
(元)和修建花圃的造价![]() (元)与修建面积
(元)与修建面积![]() (平方米)之间的函数关系分别为
(平方米)之间的函数关系分别为![]() 和
和![]() .若要求小路宽度不少于2米且不超过4米,求小路宽为多少米时修建小路和花圃的总造价最低?
.若要求小路宽度不少于2米且不超过4米,求小路宽为多少米时修建小路和花圃的总造价最低?
【答案】(1)小路的宽为2米;(2)小路的宽为2米时修建小路和花圃的总造价最低.
【解析】
(1)设小路的宽为![]() 米,根据面积公式列出方程并解方程即可;
米,根据面积公式列出方程并解方程即可;
(2)设小路的宽为![]() 米,总造价为
米,总造价为![]() 元,先分别表示出花圃的面积和小路的面积,然后根据已知函数关系,即可求出总造价为
元,先分别表示出花圃的面积和小路的面积,然后根据已知函数关系,即可求出总造价为![]() 与小路宽
与小路宽![]() 的函数关系式,化为顶点式,利用二次函数的增减性求最值即可求出此时的小路的宽.
的函数关系式,化为顶点式,利用二次函数的增减性求最值即可求出此时的小路的宽.
解:(1)设小路的宽为![]() 米,则可列方程
米,则可列方程
![]()
解得:![]() 或
或![]() (舍去)
(舍去)
答:小路的宽为2米.
(2)设小路的宽为![]() 米,总造价为
米,总造价为![]() 元,
元,
则花圃的面积为![]() 平方米,小路面积为
平方米,小路面积为![]() =
=![]() 平方米
平方米
所以![]()
整理得:![]()
∵![]() ,对称轴为x=20
,对称轴为x=20
∴当![]() 时,
时,![]() 随
随![]() 的增大而增大
的增大而增大
∴当![]() 时,
时,![]() 取最小值
取最小值
答:小路的宽为2米时修建小路和花圃的总造价最低

【题目】某校举行九年级体育锻炼考试,现随机抽取了部分学生的成绩为样本,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面两图不完整的统计图和统计表:
等级 | 成绩(分) | 频数(人数) | 频率 |
A | 45~50 | 40 | 0.4 |
B | 40~44 | 42 | x |
C | 35~39 | m | 0.12 |
D | 30~34 | 6 | 0.03 |
合计 | 1.00 |
请根据以如图表提供的信息,解答下列问题:
(1)m= ,x= ;
(2)在扇形统计图中,B等级所对应的圆心角是 度;
(3)若该校九年级共有600名学生参加了体育模板考试,请你估计成绩等级达到“优秀”的学生有 人;
(4)小明同学第一次模拟考试成绩为40分,第二次成绩为48分,则小明体育成绩提高的百分率是 %.