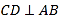Question

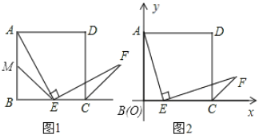
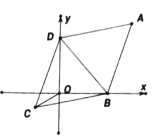
【题目】如图，在平行四边形中，是等边三角形，，且两个顶点、分别在轴，轴上滑动，连接，则的最小值是______．

Answer 1

【答案】1010.

【解析】

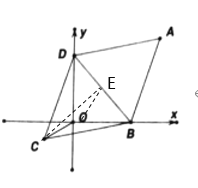
由条件可先证得△CBD是等边三角形，过点C作CE⊥BD于点E，当点C，O，E在一条直线上，此时CO最短，可求得OE和CE的长，进而得出OC的最小值.

如图所示：过点C作CE⊥BD于点E，

∵是等边三角形，

∴AB=BD=AD=20，∠BAD=60°，

∵平行四边形ABCD中，AB=CD，BC=AD，∠BAD=∠BCD=60°，

∴CD=BC=BD=20，

∴△CBD是等边三角形，∠CBD=60°，

∵CE⊥BD，△CBD是等边三角形，

∴E为BD中点，

∵∠DOB=90°，E为BD中点，

∴，

当点C，O，E在一条直线上，此时OC最短，

故CO的最小值为：CO=CEEO= CB·sin∠CBE-10=CB·sin60°-10=1010，

故答案为：1010.