题目内容
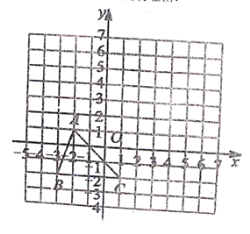
【题目】如图,抛物线C1:y=ax2+bx+4与x轴交于A(﹣3,0),B两点,与y轴交于点C,点M(﹣ ![]() ,5)是抛物线C1上一点,抛物线C2与抛物线C1关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′.
,5)是抛物线C1上一点,抛物线C2与抛物线C1关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′.
(1)求抛物线C1的解析式;
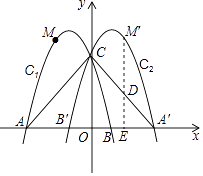
(2)过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】
(1)解:把A(﹣3,0),M(﹣ ![]() ,5)代入y=ax2+bx+4得,
,5)代入y=ax2+bx+4得,
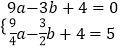 ,解得
,解得 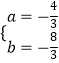 ,
,
所以抛物线C1的解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+4
x+4
(2)解:令y=0,则﹣ ![]() x2﹣
x2﹣ ![]() x+4=0,
x+4=0,
解得x1=﹣3,x2=1,
∴B(1,0),
令x=0,则y=4,∴C(0,4).
由题意,知M′( ![]() ,5),B′(﹣1,0),A′(3,0),∠CAA′=∠CA′A,
,5),B′(﹣1,0),A′(3,0),∠CAA′=∠CA′A,
∴AB′=2.
设直线A′C的解析式为y=px+q.
把A′(3,0),C(0,4)代入,
得 ![]() ,解得
,解得 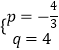 ,
,
∴y=﹣ ![]() x+4,
x+4,
当x= ![]() 时,y=﹣
时,y=﹣ ![]() ×
× ![]() +4=2,∴D(
+4=2,∴D( ![]() ,2).
,2).
由勾股定理得,AC= ![]() =5,DA′=
=5,DA′= ![]() =
= ![]() .
.
设P(m,0).
当m<3时,此时点P在点A′的左边,
若 ![]() =
= ![]() ,即有△DA′P∽△CAB′,
,即有△DA′P∽△CAB′,
∴ ![]() =
= ![]() (3﹣m),解得m=2,
(3﹣m),解得m=2,
∴P(2,0).
若 ![]() =
= ![]() ,即有△DA′P∽△B′AC,
,即有△DA′P∽△B′AC,
∴ ![]() =
= ![]() (3﹣m),解得m=﹣
(3﹣m),解得m=﹣ ![]() ,
,
∴P(﹣ ![]() ,0).
,0).
当m>3时,此时点P在点A′的右边,
∵∠CB′O≠∠DA′E,
∴∠AB′C≠∠DA′P,
∴此情况,△DA′P与△B′AC不能相似.
综上所述,存在点P(2,0)或(﹣ ![]() ,0)满足条件.
,0)满足条件.
【解析】(1)利用待定系数法,把A、M坐标代入即可;(2) 由已知条件先求出AB′=2,AC=5,再求出△DA′P中的DA′=2.5,然后分类讨论:△DA′P∽△CAB′或△DA′P∽△B′AC,由对应边成比例列出方程,求出P坐标.

【题目】某商场用13000元购进甲、乙两种矿泉水共400箱,矿泉水的成本价与销售价如下表所示:
类别 | 成本价/(元·箱 | 销售价/(元·箱 |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这400箱矿泉水,可获利多少元?
【题目】某地某一时刻的地面温度是26℃,每升高![]() ,温度下降6℃,下面是温度(℃)与距离地面的高度
,温度下降6℃,下面是温度(℃)与距离地面的高度![]() 对应的数值:
对应的数值:
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 26 | 20 | 14 | 8 |
|
| … |
根据上表,请完成下面的问题.
(1)表中![]() ;
;
(2)直接写出温度![]() 与高度
与高度![]() 之间的函数关系式,并写出其中的常量和变量;
之间的函数关系式,并写出其中的常量和变量;
(3)求该地距地面![]() 处的温度.
处的温度.