题目内容
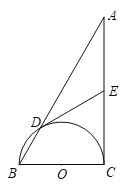
【题目】已知四边形ABCD是平行四边形,CD为⊙O的切线,点C是切点.
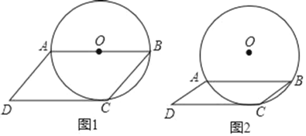
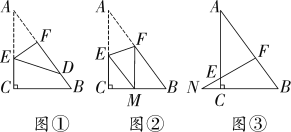
(1)如图1,若AB为⊙O直径,求四边形ABCD各内角的度数;
(2)如图2,若AB为弦,⊙O的半径为3cm,当BC=2cm时,求CD的长.
【答案】(1)∠DAB=∠DCB=135°,∠D=∠B=45°;(2)![]() cm.
cm.
【解析】
(1)如图1中,连接OC.只要证明△OCB是等腰直角三角形即可解决问题,
(2)如图2中,连接OC交AB于点E,连接OB,由(1)可知:AB⊥OC,设OE=xcm,则CE=(3-x)cm,构建方程求解,再利用垂径定理即可解决问题.
解:(1)如图1中,连接OC.
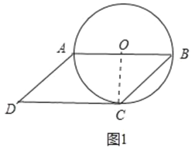
∵CD切⊙O于点C,
∴CD⊥OC,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴AB⊥OC,
∵OC=OB,
∴∠B=∠OCB=45°,
∴∠BCD=∠OCD+∠OCB=135°,
∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB=135°,∠D=∠B=45°.
(2)如图2中,连接OC交AB于点E,连接OB,
由(1)可知:AB⊥OC,

∴OB2﹣OE2=BE2,BC2﹣CE2=EB2,
设OE=xcm,则CE=(3﹣x)cm,
![]() OB=3,BC=2,
OB=3,BC=2,
∴32﹣x2=22﹣(3﹣x)2,
∴x=![]() ,即OE=
,即OE=![]() cm,
cm,
∴BE=![]() =
=![]() cm,
cm,
∴AB=2BE=![]() cm,
cm,
∵四边形ABCD 平行四边形,
∴CD=AB=![]() cm.
cm.

 轻松课堂单元期中期末专题冲刺100分系列答案
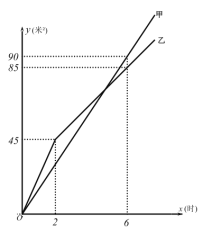
轻松课堂单元期中期末专题冲刺100分系列答案【题目】服装店准备购进甲乙两种服装共100件,费用不得超过7500元.甲种服装每件进价80元,每件售价120元;乙种服装每件进价60元,每件售价90元.
(Ⅰ)设购进甲种服装![]() 件,试填写下表.
件,试填写下表.
表一
购进甲种服装的数量/件 | 10 | 20 | … |
|
购进甲种服装所用费用/元 | 800 | 1600 | … | |
购进乙种服装所用费用/元 | 5400 | … |
表二
购进甲种服装的数量/件 | 10 | 20 | … |
|
甲种服装获得的利润/元 | 800 | … | ||
乙种服装获得的利润/元 | 2700 | 2400 | … |
(Ⅱ)给出能够获得最大利润的进货方案,并说明理由.