题目内容
【题目】如图,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是( )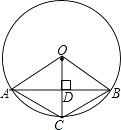
A.AD=BD
B.OD=CD
C.∠CAD=∠CBD
D.∠OCA=∠OCB
【答案】B
【解析】∵在⊙O中,AB是弦,半径OC⊥AB,
∴AD=DB,
当DO=CD,
则AD=BD,DO=CD,AB⊥CO,
故四边形OACB为菱形.
所以答案是:B.
【考点精析】关于本题考查的菱形的判定方法和垂径定理,需要了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能得出正确答案.

练习册系列答案
相关题目