题目内容
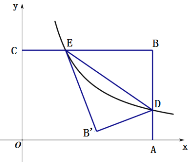
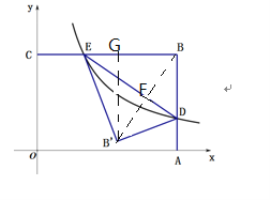
【题目】如图,平面直角坐标系xOy中,线段BC∥x轴、线段AB∥y轴,点B坐标为(4,3),反比例函数y=![]() (x>0)的图像与线段AB交于点D,与线段BC交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,则点B'的纵坐标是( )
(x>0)的图像与线段AB交于点D,与线段BC交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,则点B'的纵坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
先根据矩形的性质和点B坐标把D、E的坐标计算出来,再计算BE、BD、ED的长度,利用对称和等面积法把BF的长度计算出来,最后根据勾股定理计算即可得到答案;
解:∵四边形OABC是矩形,
∴CB∥x轴,AB∥y轴,
∵点B坐标为(4,3),
∴D的横坐标为4,E的纵坐标为3,
∵D、E在反比例函数y=![]() (x>0)的图像上,
(x>0)的图像上,
∴D的坐标为:(4,1),E的坐标为:(![]() ,3),
,3),
∴BE=4-![]() =
= ![]() , BD=3-1=2,
, BD=3-1=2,
∴![]() ,
,
连接BB′,交ED于F,过B′作B′G⊥BC于G,如图:
∵B,B′关于ED对称,
∴BF=B′F,BB′⊥ED,
∴BFED=BEBD,
即:![]() ,
,
∴![]() ,
,
∴BB′=![]() ,
,
设EG=x,则BG=![]() -x,
-x,
![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴EG![]() ,
,
∴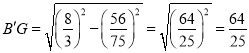 ,
,
则点B'的纵坐标为:![]() ,
,
故选B.

练习册系列答案
相关题目
【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了![]() 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:

学生最喜欢的节目人数条形统计图
节目 | 人数( 名 ) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 |
|
中国诗词大会 |
| 40% |
出彩中国人 | 10 | 20% |
学生最喜爱的节目人数统计表
根据以上提供的信息,解答下列问题:
(1)![]() =
= ![]() =
= ![]() = ;
= ;
(2)补全条形统计图;
(3)若该校共有学生1200名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名?