Question

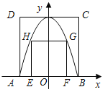
【题目】如图，AB是⊙O 的直径，CD是⊙O的一条弦，且CD⊥AB于点E．

（1）求证：∠BCO=∠D；

（2）若CD=，AE=2，求⊙O的半径．

Answer 1

【答案】（1）见解析；（2）3．

【解析】

试题根据OC=OB得到∠BCO=∠B，根据弧相等得到∠B=∠D，从而得到答案；根据题意得出CE的长度，设半径为r，则OC=r，OE=r－2，根据Rt△OCE的勾股定理得出半径．

试题解析：（1）证明：∵ OC=OB，∴ ∠BCO=∠B ∵， ∴ ∠B=∠D， ∴ ∠BCO=∠D．

（2）解：∵AB是⊙O的直径，CD⊥AB， ∴ CE=．

在Rt△OCE中，OC2=CE2+OE2， 设⊙O的半径为r，则OC=r，OE=OA－AE=r－2，

∴，解得：r=3， ∴⊙O的半径为3