题目内容
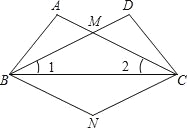
【题目】如图,已知AB=DC,AC=DB,AC与DB交于点M.过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N.
(1)求证:△ABC≌△DCB;
(2)求证:四边形BNCM是菱形.

【答案】证明见解析.
【解析】
试题分析:(1)利用SSS定理可直接判定△ABC≌△DCB;
(2)首先根据CN∥BD、BN∥AC,可判定四边形BNCM是平行四边形,再根据△ABC≌△DCB可得∠1=∠2,进而可得BM=CM,根据邻边相等的平行四边形是菱形可得结论.
试题解析:(1)∵在△ABC和△DCB中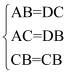 ,∴△ABC≌△DCB(SSS);
,∴△ABC≌△DCB(SSS);
(2)∵CN∥BD、BN∥AC,
∴四边形BNCM是平行四边形,
∵△ABC≌△DCB,
∴∠1=∠2,
∴BM=CM,
∴四边形BNCM是菱形.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目