题目内容
【题目】将已知六边形ABCDEF，用对角线将它剖分成互不重叠的4个三角形，那么各种不同的剖分方法种数是（ ）
A.6
B.8
C.12
D.14
【答案】D
【解析】解答：∵六边形ABCDEF有6个顶点，且用对角线将它剖分成互不重叠的4个三角形， ∴只能通过同一个顶点作三条对角线（如图1），这种分法有6种，
也从一个顶点作两条对角线（如图2），这种分法有2种，
如图3，中间是个四边形，两端2个三角形，把四边形加条对角线，这种分法有6种，
故各种不同的剖分方法有14种．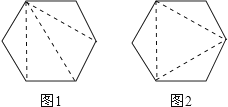
分析：本题考查了多边形的对角线，n边形过一个顶点有（n-3）条对角线，它们把n边形分割成了（n-2）个三角形．
【考点精析】解答此题的关键在于理解多边形的对角线的相关知识，掌握设多边形的边数为n，则多边形的对角线条数为n(n-3)/2．
练习册系列答案
相关题目
【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售，其进价与售价如下表：
进价（元/台） | 售价（元/台） | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
（1）一季度，橱具店购进这两种电器共30台，用去了5600元，并且全部售完，问橱具店在该买卖中赚了多少钱？
（2）为了满足市场需求，二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台，且电饭煲的数量不少于电压锅的 
，橱具店有哪几种进货方案？并说明理由.
（3）在（2）的条件下，直接写出橱具店赚钱最多的进货方案.
