Question

【题目】如图所示，个直角边长为3的等腰直角三角形，……，斜边在同一直线上，设的面积为，的面积为…，的面积为，则_________________；_____________．

Answer 1

【答案】

【解析】

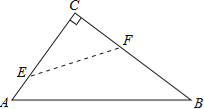
连接B1、B2、B3、B4、B5点，显然它们共线且平行于AC1，依题意可知△B1C1B2是等腰直角三角形，知道△B1B2D1与△C1AD1相似，求出相似比，根据三角形面积公式可得出S1，同理：B2B3：AC2=1：2，所以B2D2：D2C2=1：2，所以S2=，同样的道理，即可求出S3，S4…Sn．

∵n+1个边长为1的等腰三角形有一条边在同一直线上，
∴S△AB1C1=，
连接B1、B2、B3、B4、B5点，根据等腰三角形性质和平行线判定，它们共线且平行于AC1
∵∠B1C1B2=90°
∴A1B1∥B2C1
∴△B1C1B2是等腰直角三角形，且边长=1，
∴△B1B2D1∽△C1AD1，
∴B1D1：D1C1=1：1，
∴S1=，
故答案为：；
同理：B2B3：AC2=1：2，
∴B2D2：D2C2=1：2，
∴S2=，
同理：B3B4：AC3=1：3，
∴B3D3：D3C3=1：3，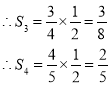
，
…
∴Sn=

故答案为：．