��Ŀ����
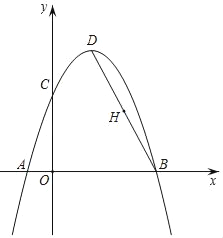
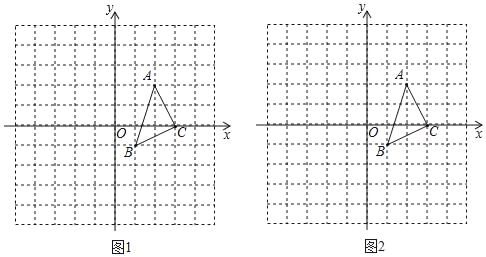
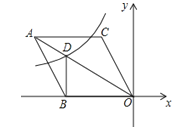
����Ŀ����ͼ1��ijУ��һ�����οյ�ABCD����A=60�㣬AB=40m���ּƻ����ڲ���һ���ĸ�����ֱ����������������ϵľ������EFGH�����ಿ���ֻ��ݣ��ֹ�˾����أ���ƺ�����Ϊy��Ԫ���������s��m2��֮��ĺ�����ϵ��ͼ2��ʾ����AEΪx�ף�
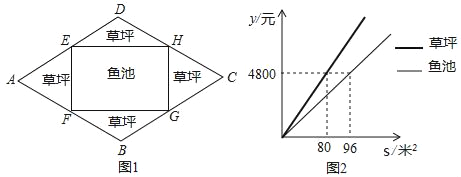
��1����գ�ED=�� ��m��EH=�� ��m�����ú�x�Ĵ���ʽ��ʾ����
����ʾ����ֱ���������У�30������Ե�ֱ�DZߵ���б�ߵ�һ�룩
��2�����������EFGH�������300![]() m2����EF�ij��ȣ�
m2����EF�ij��ȣ�
��3��EF�ij���Ϊ����ʱ��������غͲ�ƺ���������ͣ�������Ϊ����Ԫ��
���𰸡���1��![]() ��
��![]() �� ��2��10m��30m����3��x=20ʱ���������С����СֵΪ
�� ��2��10m��30m����3��x=20ʱ���������С����СֵΪ![]() Ԫ��
Ԫ��
��������
(1)ֱ��д���������.
(2)����DB���ж���AEFΪ�ȱ������Σ��Ӷ�EF=x������(1)��EH�ij������ݾ��������ʽ�г����̣����x����.
(3)����ͼ2�ó���ƺ����صļۣ��ֱ������ƺ����ص����(�ú�x��ʽ�ӱ�ʾ)���Ӷ��õ�һ���ܼ�Ϊһ������x���κ���������д�ɶ���ʽ����ɵó���������ֵ.
��1��![]() ��
��![]() ��
��
��2������![]() ����EF��DB
����EF��DB
��![]()
�� ![]()
��![]()
��![]()
���![]() �ǵȱ�������
�ǵȱ�������
��![]()
�ɣ�1����֪![]()
��![]()
![]()
![]()
���![]() ��
��![]() ��������������⣬
��������������⣬
��![]() �ij���10
�ij���10![]() ��30
��30![]() ��
��
��3��������ò�ƺ����Ϊ��4800��80=60Ԫ/��2��
��ص���Ϊ��4800��96=50Ԫ/��2��
���ı���ABCD�����Σ���BAD=60�㣬AB=40m����BD=40��AC=![]() ��
��
������ABCD������ǣ�![]()
![]() ��
��
�߾���EFGH������ǣ�![]()
���ƺ������ǣ�![]()
�������![]()
![]()
![]()
��![]()
�൱![]() ʱ���������С����СֵΪ
ʱ���������С����СֵΪ![]() Ԫ
Ԫ
��EF�ij���Ϊ20mʱ��������غͲ�ƺ���������ͣ�������![]() Ԫ��
Ԫ��
�ʴ�Ϊ����1��![]() ��
��![]() �� ��2��10m��30m����3��x=20ʱ���������С����СֵΪ
�� ��2��10m��30m����3��x=20ʱ���������С����СֵΪ![]() Ԫ.
Ԫ.