题目内容
【题目】如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连结HN.则在点M运动过程中,线段HN长度的最小值是( )
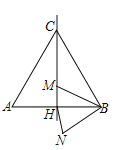
A.6B.3C.2D.1.5
【答案】B
【解析】
取CB的中点G,连接MG,根据等边三角形的性质可得BH=BG,再求出∠HBN=∠MBG,根据旋转的性质可得MB=NB,然后利用“边角边”证明△MBG≌△NBH,再根据全等三角形对应边相等可得HN=MG,然后根据垂线段最短可得MG⊥CH时最短,再根据∠BCH=30°求解即可.
解:如图,取BC的中点G,连接MG,
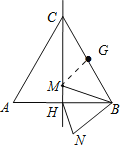
∵旋转角为60°,
∴∠MBH+∠HBN=60°,
又∵∠MBH+∠MBC=∠ABC=60°,
∴∠HBN=∠GBM,
∵CH是等边△ABC的对称轴,
∴HB=![]() AB,
AB,
∴HB=BG,
又∵MB旋转到BN,
∴BM=BN,
在△MBG和△NBH中,
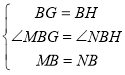 ,
,
∴△MBG≌△NBH(SAS),
∴MG=NH,
根据垂线段最短,当MG⊥CH时,MG最短,即HN最短,
此时∠BCH=![]() ×60°=30°,CG=
×60°=30°,CG=![]() AB=
AB=![]() ×12=6,
×12=6,
∴MG=![]() CG=
CG=![]() ×6=3,
×6=3,
∴HN=3;
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目