题目内容
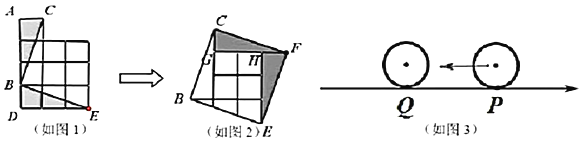
【题目】如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H,得到的四边形EFGH叫中点四边形.
(1)求证:四边形EFGH是平行四边形;
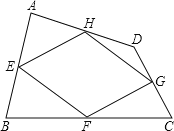
(2)如图,当四边形ABCD变成等腰梯形时,它的中点四边形是菱形,请你探究并填空:
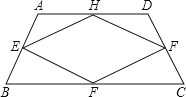
当四边形ABCD变成平行四边形时,它的中点四边形是 ;
当四边形ABCD变成矩形时,它的中点四边形是 ;
当四边形ABCD变成菱形时,它的中点四边形是 ;
当四边形ABCD变成正方形时,它的中点四边形是 ;
(3)根据以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
【答案】(1)相等;(2)垂直;(3)见解析.
【解析】
(1)连接BD.利用三角形中位线定理推出所得四边形对边平行且相等,故为平行四边形;
(2)连接AC、BD.根据三角形的中位线定理,可以得到所得四边形的两组对边分别和原四边形的对角线平行,且分别等于原四边形的对角线的一半,再根据矩形、菱形、正方形的判定方法进行判定即可
(3)由(2)可知,中点四边形的形状是由原四边形的对角线的关系决定的.
(1)证明:连接BD.
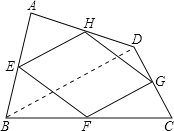
∵E、H分别是AB、AD的中点,
∴EH是△ABD的中位线.
∴EH=![]() BD,EH∥BD.
BD,EH∥BD.
同理得FG=![]() BD,FG∥BD.
BD,FG∥BD.
∴EH=FG,EH∥FG.
∴四边形EFGH是平行四边形.
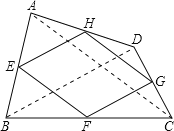
(2)连接AC、BD.根据三角形的中位线定理,可以得到所得四边形的两组对边分别和原四边形的对角线平行,且分别等于原四边形的对角线的一半.
若顺次连接对角线相等的四边形各边中点,则所得的四边形的四条边都相等,故所得四边形为菱形;
若顺次连接对角线互相垂直的四边形各边中点,则所得的四边形的四个角都是直角,故所得四边形为矩形;
若顺次连接对角线相等且互相垂直的四边形各边中点,则综合上述两种情况,故所得的四边形为正方形;
故答案为:平行四边形,菱形,矩形,正方形;
(3)中点四边形的形状是由原四边形的对角线的关系决定的.