题目内容
已知有理数A,B,x,y满足A+B≠0,且(A+B):(A-B)=(2x+y):(x-y),那么A:(A+B)=
- A.3x:(2x+y)
- B.3x:(4x+2y)
- C.x:(x+y)
- D.2x:(2x+y)
B
分析:可设A+B=(2x+y)k,进而用k表示出A-B,联立求得A的值,代入所给代数式中求解即可.
解答:设A+B=(2x+y)k,则A-B=(x-y)k,
∴A= xk,
xk,
∴A:(A+B)= xk:(2x+y)k=3x:(4x+2y),
xk:(2x+y)k=3x:(4x+2y),
故选B.
点评:考查比例性质的应用;用含k的代数式表示出A+B及A的值是解决本题的突破点.
分析:可设A+B=(2x+y)k,进而用k表示出A-B,联立求得A的值,代入所给代数式中求解即可.
解答:设A+B=(2x+y)k,则A-B=(x-y)k,
∴A=
 xk,
xk,∴A:(A+B)=
 xk:(2x+y)k=3x:(4x+2y),
xk:(2x+y)k=3x:(4x+2y),故选B.
点评:考查比例性质的应用;用含k的代数式表示出A+B及A的值是解决本题的突破点.

练习册系列答案
相关题目


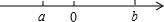 已知有理数a,b所对应的点在数轴上如图所示,化简|b-a|得( )
已知有理数a,b所对应的点在数轴上如图所示,化简|b-a|得( )