ΧβΡΩΡΎ»ί
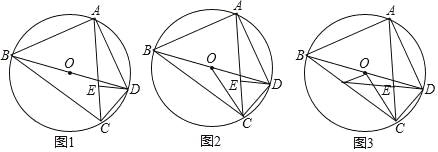
ΓΨΧβΡΩΓΩΘ®±ΨΧβ¬ζΖ÷8Ζ÷Θ©ΓΑ«– ΒΦθ«α―ß…ζΩΈ“ΒΗΚΒΘΓ± «Έ“ –Ής“ΒΗΡΗοΒΡ“Μœν÷Ί“ΣΨΌ¥κΘ°Ρ≥÷–―ßΈΣΝΥΫβ±Ψ–Θ―ß…ζΤΫΨυΟΩΧλΒΡΩΈΆβΉς“Β ±ΦδΘ§ΥφΜζ≥ι»Γ≤ΩΖ÷―ß…ζΫχ––Έ ΨμΒς≤ιΘ§≤ΔΫΪΒς≤ιΫαΙϊΖ÷ΈΣAΓΔBΓΔCΓΔDΥΡΗωΒ»ΦΕΘ°AΘΚ1–Γ ±“‘ΡΎΘ§BΘΚ1–Γ ±-1Θ°5–Γ ±Θ§CΘΚ1Θ°5–Γ ±-2–Γ ±Θ§DΘΚ–Γ ±“‘…œΘ°ΗυΨίΒς≤ιΫαΙϊΜφ÷ΤΝΥ»γΆΦΥυ ΨΒΡΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ°«κΗυΨίΆΦ÷––≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
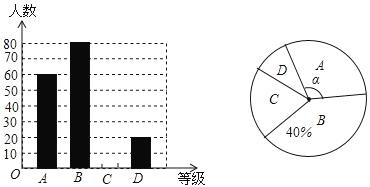
Θ®1Θ©ΗΟ–ΘΙ≤Βς≤ιΝΥ_________Οϊ―ß…ζΘΜ
Θ®2Θ©«κΫΪΧθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©±μ ΨΒ»ΦΕAΒΡ…»–Έ‘≤–ΡΫ«![]() ΒΡΕ» ΐ «____________ΘΜ
ΒΡΕ» ΐ «____________ΘΜ
Θ®4Θ©‘Ύ¥Υ¥ΈΈ ΨμΒς≤ι÷–Θ§ΦΉΓΔ““ΝΫΑύΗς”–2»ΥΤΫΨυΟΩΧλΩΈΆβΉς“Β ±ΦδΕΦ «2–Γ ±“‘…œΘ§¥”’β4»Υ÷–»Έ―Γ2»Υ»Ξ≤ΈΦ”ΉυΧΗΘ§”ΟΝ–±μΜρ ςΉ¥ΆΦΒΡΖΫΖ®«σ―Γ≥ωΒΡ2»Υά¥Ή‘≤ΜΆ§ΑύΦΕΒΡΗ≈¬ Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©200»ΥΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©![]() ΘΜΘ®4Θ©
ΘΜΘ®4Θ©![]() ΘΜ
ΘΜ
ΓΨΫβΈωΓΩ
‘ΧβΘ®1Θ©¥”Χθ–ΈΆΦ÷–Έ“Ο«Ω…“‘Ω¥ΒΟ≥ωAΒΡ»Υ ΐΈΣ60Θ§BΒΡ»Υ ΐΈΣ80Θ§DΒΡ»Υ ΐΈΣ20ΘΜ¥”…»–ΈΆ≥ΦΤΆΦ÷–Έ“Ο«ΡήΩ¥ΒΫB’ΦΒΡ±»άΐ40%Θ§’β―υΈ“Ο«Κή»ί“ΉΨΆΡήΒΟ≥ωΙ≤Βς≤ιΝΥ200»ΥΘΜ
Θ®2Θ©ΫχΕχΨΆΡήΒΟ≥ωCΒΡ»Υ ΐ40»ΥΘ®ΆΦ–ΈΩ…“‘Ή‘––≤Ι≥δΘ©ΘΜ
Θ®3Θ©A’ΦΒΡ±»÷ΊΦ¥…»–Έ‘≤–ΡΫ«![]() ΒΡΕ» ΐΈΣΘΚ
ΒΡΕ» ΐΈΣΘΚ![]() =
=![]() ΘΜ
ΘΜ
ΦΉ““ΝΫΑύΒΡ―ß…ζΈ“Ο«Ζ÷±π±ξ ΨΈΣΦΉAΓΔΦΉBΓΔ““AΓΔ““BΘ§‘ρ“ΜΙ≤”–![]() ΚΆ
ΚΆ![]() ΓΔ
ΓΔ![]() ΚΆ
ΚΆ![]() ΓΔ
ΓΔ![]() ΚΆ
ΚΆ![]() ΓΔ
ΓΔ![]() ΚΆ
ΚΆ![]() ΓΔ
ΓΔ![]() ΚΆ
ΚΆ![]() ΓΔ
ΓΔ![]() ΚΆ
ΚΆ![]() Θ°’β―υΈ“Ο«ΨΆΚή»ί“ΉΒΟ≥ωΝΫ»Υά¥Ή‘≤ΜΆ§ΑύΦΕΒΡΗ≈¬ ΈΣΘΚ
Θ°’β―υΈ“Ο«ΨΆΚή»ί“ΉΒΟ≥ωΝΫ»Υά¥Ή‘≤ΜΆ§ΑύΦΕΒΡΗ≈¬ ΈΣΘΚ![]()
‘ΧβΫβΈωΘΚΘ®1Θ©ΫβΘΚΘ®1Θ©200ΘΜΘ®2Θ©≤ΙΆΦ»γœ¬ΘΚ

Θ®2Θ©ΫβΘΚ60Γ¬200=30%Θ°
Θ®3Θ©ΫβΘΚ…ηΦΉΑύ―ß…ζΈΣ![]() Θ§
Θ§![]() ΘΜ‘ρΥυ”–Ω…ΡήΒΡ«ιΩωΈΣΘ®
ΘΜ‘ρΥυ”–Ω…ΡήΒΡ«ιΩωΈΣΘ®![]() Θ©Θ§Θ®
Θ©Θ§Θ®![]() Θ©Θ§
Θ©Θ§
Θ®![]() Θ©Θ§
Θ©Θ§![]() Θ©Θ§
Θ©Θ§![]() Θ§
Θ§![]() Νυ÷÷«ιΩωΘ°Υυ“‘≤Μ‘ΌΆ§“ΜΑύΒΡ«ιΩω”–ΥΡ÷÷Θ§Η≈¬ ΈΣ
Νυ÷÷«ιΩωΘ°Υυ“‘≤Μ‘ΌΆ§“ΜΑύΒΡ«ιΩω”–ΥΡ÷÷Θ§Η≈¬ ΈΣ![]() Θ°
Θ°