Question

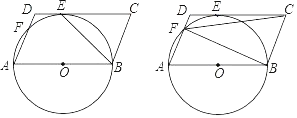
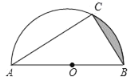
【题目】如图，已知AB是⊙O的直径，点C在⊙O上，∠CAB＝30°，AC＝3，则图中阴影部分的面积是（　　）

A. B. C. D.

Answer 1

【答案】A

【解析】

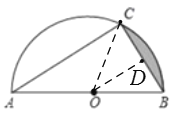
连接OC，过点O作OD⊥BC，垂足为D，由已知可得△OCB是等边三角形，边长为3，求出△OCB的面积以及扇形COB的面积即可求得阴影部分的面积.

连接OC，过点O作OD⊥BC，垂足为D，

则∠ODB=90°，

∵AB是⊙O的直径，

∴∠ACB=90°，

∴∠ODB=∠ACB，

∴OD//AC，

∴∠BOD=∠BAC=30°，

∴∠OBC=90°-∠BOD=60°，BO=2BD，

又∵AO=OB=OC，

∴OD=AC=，△OBC是等边三角形，

在Rt△OBD中，OB2=BD2+OD2，

∴BD=，OB=3，

∴△COB的面积＝，

∴扇形COB的面积＝，

所以图中阴影部分的面积＝，

故选A．