题目内容
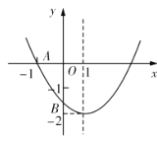
【题目】如图,已知抛物线![]()
![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于
轴相交于![]() 点,对称轴为
点,对称轴为![]() ,直线
,直线![]() 与抛物线相交于
与抛物线相交于![]() 、
、![]() 两点.
两点.
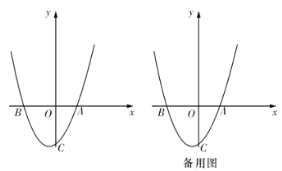
(1)求此抛物线的解析式;
(2)![]() 为抛物线上一动点,且位于
为抛物线上一动点,且位于![]() 的下方,求出
的下方,求出![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标;
的坐标;
(3)设点![]() 在
在![]() 轴上,且满足
轴上,且满足![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;
;
(2)当![]() 时,
时,![]() 取最大值
取最大值![]() ,此时
,此时![]() 点坐标为
点坐标为![]() .
.
(3)![]() 或17.
或17.
【解析】
(1)根据对称轴与点A代入即可求解;
(2)先求出![]() ,过
,过![]() 点作
点作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,设
,设![]() ,得到
,得到![]() ,
,![]() ,表示出
,表示出![]() ,根据二次函数的性质即可求解;
,根据二次函数的性质即可求解;
(3)根据题意分①当![]() 在
在![]() 轴正半轴上时, ②当
轴正半轴上时, ②当![]() 在
在![]() 轴负半轴上时利用相似三角形的性质即可求解.
轴负半轴上时利用相似三角形的性质即可求解.
(1)∵对称轴为x=1,
∴![]() =1,
=1,
∴b=2a,
∴y=ax2+2ax5,
∵y=x+3与x轴交于点A(3,0),
将点A代入y=ax2+2ax5可得a=![]()
∴![]() .
.
(2)令![]() ,解得:
,解得:![]() ,
,![]() ,
,
∴![]() ,
,
过![]() 点作
点作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,
则![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() 取最大值
取最大值![]() ,
,
此时![]() 点坐标为
点坐标为![]() .
.
(3)存在,
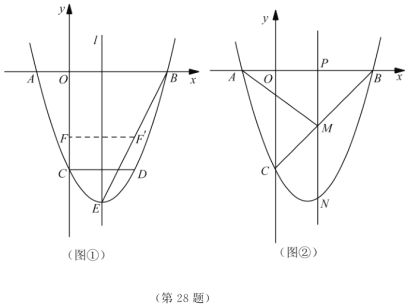
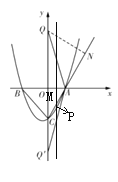
理由:①当![]() 在
在![]() 轴正半轴上时,如图,
轴正半轴上时,如图,
过点![]() 作
作![]() 于
于![]() ,
,
根据三角形的外角的性质得,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
②当![]() 在
在![]() 轴负半轴上时,记作
轴负半轴上时,记作![]() ,
,
由①知,![]() ,取
,取![]() ,如图,
,如图,
则由对称知:![]() ,
,
∴![]() ,
,
因此点![]() 也满足题目条件,∴
也满足题目条件,∴![]() ,
,
综合以上得:![]() 或17.
或17.

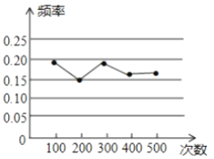
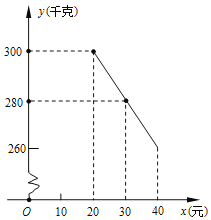
【题目】某校为了解七、八年级学生英语听力训练情况(七、八年级学生人数相同),某周从这两个年级学生中分别随机抽查了30名同学,调查了他们周一至周五的听力训练情况,根据调查情况得到如下统计图表:
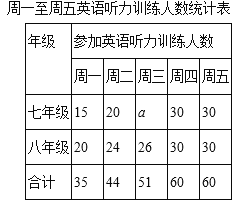

(1)填空:a= ;
(2)根据上述统计图表完成下表中的相关统计量:
年级 | 平均训练时间的中位数 | 参加英语听力训练人数的方差 |
七年级 | 24 | 34 |
八年级 |
| 14.4 |
(3)请你利用上述统计图表对七、八年级英语听力训练情况写出两条合理的评价;
(4)请你结合周一至周五英语听力训练人数统计表,估计该校七、八年级共480名学生中周一至周五平均每天有多少人进行英语听力训练.