题目内容
【题目】已知:如图,![]() 是半圆
是半圆![]() 的直径,弦
的直径,弦![]() ,动点
,动点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且
上,且![]() ,
,![]() 的延长线与射线
的延长线与射线![]() 相交于点
相交于点![]() 、与弦
、与弦![]() 相交于点
相交于点![]() (点
(点![]() 与点
与点![]() 、
、![]() 不重合),
不重合),![]() ,
,![]() .设
.设![]() ,
,![]() 的面积为
的面积为![]() .
.

(1)求证:![]() ;
;
(2)求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围
的取值范围
(3)当![]() 是直角三角形时,求线段
是直角三角形时,求线段![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() (
(![]() <x<10).
<x<10).
(3)线段OP的长为8.
【解析】
试题分析:(1)连接OD,通过证明△AOP≌△ODQ后即可证得AP=OQ;
(2)作PH⊥OA,根据cos∠AOC=![]() 得到OH=PO=x,从而得到S△AOP=AOPH=3x,利用三角形相似得当对应
得到OH=PO=x,从而得到S△AOP=AOPH=3x,利用三角形相似得当对应
边的比相等即可得到函数解析式;
(3)分类讨论:当∠POE=90°时、当∠OPE=90°时、当∠OEP=90°时三种情况讨论即可得到正确的结论.
试题解析:(1)连接OD,在△AOP和△ODQ中,∵OC=OD,∴∠OCD=∠ODC,∵![]() ,∴∠OCD=∠COA,∠POA=∠QDO.在△AOP和△ODQ中,
,∴∠OCD=∠COA,∠POA=∠QDO.在△AOP和△ODQ中,
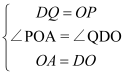 ,∴△AOP≌△ODQ,∴AP=OQ;
,∴△AOP≌△ODQ,∴AP=OQ;
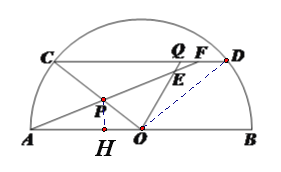
(2)作PH⊥OA交OA于H,∵cos∠AOC=![]() ,∴OH=
,∴OH= ![]() PO=
PO= ![]() x,PH=
x,PH=![]() x,
x,
∴S△AOP= ![]() AOPH=3x,∵
AOPH=3x,∵![]() ,∴△PFC∽△PAO,
,∴△PFC∽△PAO,![]() ,
,
∴![]() ,当点F与点D 重合时,∵CD=2OC cos∠OCD=2×10×
,当点F与点D 重合时,∵CD=2OC cos∠OCD=2×10×![]() =16,
=16,
解得x=![]() ,∴
,∴![]() (
(![]() <x<10);
<x<10);
(3)当∠POE=90°时,CQ= ![]() ,∴PO=DQ=CD﹣CQ=
,∴PO=DQ=CD﹣CQ= ![]() ,∵
,∵![]() <x<10,∴PO=
<x<10,∴PO=![]() (舍);
(舍);
当∠OPE=90°时,∠OPA=90°,∴PO=AOcos∠COA=8;
当∠OEP=90°时,∵![]() ,∴∠AOQ=∠DQO=∠APO,∴∠AOP=∠AEO=90°,此时弦CD不存在,此种情况不符合题意,舍;
,∴∠AOQ=∠DQO=∠APO,∴∠AOP=∠AEO=90°,此时弦CD不存在,此种情况不符合题意,舍;
综上,线段OP的长为8.

练习册系列答案
相关题目