题目内容
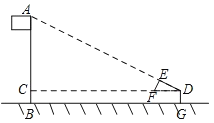
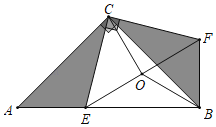
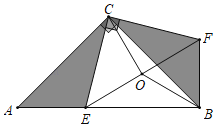
【题目】如图,等腰Rt△ABC,AB=6,点E是斜边AB上的一点(端点A、B除外),将△CAE绕C逆时针旋转90°至△CBF,连接EF,且EF的中点为O,连OB、OC,设AE=x,
(1)求证:OB=OC;
(2)用x表示△BEF的面积S△BEF,并求S△BEF的最大值;
(3)用x表示四边形BECF的周长C,并求C的最小值.
【答案】(1)详见解析;(2)![]() ;(3)12.
;(3)12.
【解析】
(1)由旋转的性质和等腰直角三角形的性质可得∠ECF=90°,∠EBF=90°,然后再由直角三角形的性质可得结论;
(2)由三角形面积公式可求得S△BEF与x的关系式,然后根据二次函数的性质求解即可;
(3)易得四边形BECF的周长C=6+2CE,于是当CE⊥AB时,CE的值最小,亦即四边形BECF的周长C最小,然后由等腰直角三角形的性质求解即可.
解:(1)证明:∵Rt△ABC是等腰直角三角形,∴AC=BC,∠ACB=90°,∴∠CAB=∠CBA=45°,
∵将△CAE绕C逆时针旋转90°至△CBF,
∴∠A=∠CBF=45°,AE=BF,CE=CF,∠ECF=90°,
∴∠EBF=∠ABC+∠CBF=90°,
∵EF的中点为O,∴CO=![]() EF,BO=
EF,BO=![]() EF,
EF,
∴BO=CO;
(2)∵AE=BF=x,AB=6,∴BE=6﹣x,
∴S△BEF=![]() BE×BF=﹣
BE×BF=﹣![]() x2+3x=﹣
x2+3x=﹣![]() (x﹣3)2+
(x﹣3)2+![]() ,
,
∴当x=3时,S△BEF的最大值为![]() ;
;
(3)∵四边形BECF的周长C=BE+BF+CE+CF=BE+AE+2CE=6+2CE,
∴当CE的值最小时,四边形BECF的周长C有最小值,
∴当CE⊥AB时,CE的值最小,此时CE=![]() AB=3,
AB=3,
∴四边形BECF的周长C最小值=6+2×3=12.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目