题目内容
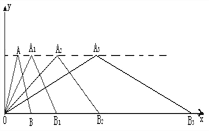
【题目】如下图所示,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3, 已知A(1,3),A1 (2,3), A2 (4,3), A3 (8,3),B(2,0), B1 (4,0), B2 (8,0), B3 (16,0),观察每次变换前后的三角形有何变化,找出规律,按此变换规律将△OA3B3变换成△OAnBn, ,则An的坐标是_______ ,Bn的坐标是_________ .
.
【答案】2n,3;2n+1,0
【解析】试题分析:观察不难发现,点A系列的横坐标是2的指数次幂,指数为脚码,纵坐标都是3;点B系列的横坐标是2的指数次幂,指数比脚码大1,纵坐标都是0,根据此规律写出即可.
解:∵A(1,3),A1(2,3),A2(4,3),A3(8,3),
2=21、4=22、8=23,
∴An(2n,3),
∵B(2,0),B1(4,0),B2(8,0),B3(16,0),
2=21、4=22、8=23,16=24,
∴Bn(2n+1,0).
故答案为:2n,3;2n+1,0.

练习册系列答案
相关题目