题目内容
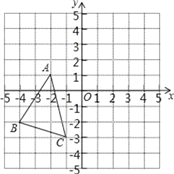
【题目】如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)
(1)A′、B′两点的坐标分别为A′ 、B′ ;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△A′B′C′的面积.
【答案】(1)A′(3,5)、B′(1,2);(2)作图见解析;(3)5.5.
【解析】试题分析:(1)由点C(-1,-3)与点C′(4,1)是对应点,得出平移规律为:向右平移5个单位,向上平移4个单位,按平移规律即可写出所求的点的坐标;
(2)按平移规律作出A、B的对应点A′,B′,顺次连接A′、B′、C′,即可得到△A′B′C′;
(3)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积即可求解.
试题解析:(1)∵△A′B′C′是△ABC平移之后得到的图象,并且C(-1,-3)的对应点C′的坐标为(4,1),
∴平移前后对应点的横坐标加5,纵坐标加4,
∴△ABC先向右平移5个单位,再向上平移4个单位得到△A′B′C′,
∵A(-2,1),B(-4,-2),
∴A′(3,5)、B′(1,2);
(2)△A′B′C′如图所示;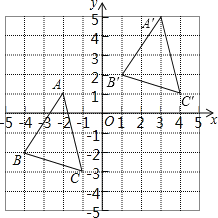

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目