题目内容
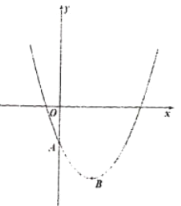
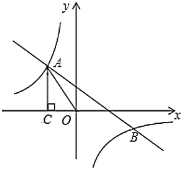
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第二、四象限内的点
的图象交于第二、四象限内的点![]() 和点
和点![]() .过点
.过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,
,![]() 的面积为4.若在
的面积为4.若在![]() 轴上取点
轴上取点![]() ,则当
,则当![]() 取得最大值时,点
取得最大值时,点![]() 的坐标为______.
的坐标为______.
【答案】![]()
【解析】
由△AOC的面积为4,可求出a的值,确定反比例函数的关系式,把点B坐标代入反比例函数解析式可求b的值.作点B关于x轴的对称点B′,则直线AB′与x轴交点就是所求的点P,求出直线与x轴的交点坐标即可.
解:∵点A(a,4),
∴AC=4,
∵S△AOC=4,即![]() OCAC=4,
OCAC=4,
∴OC=2,
∵点A(a,4)在第二象限,
∴a=-2,A(-2,4),
将A(-2,4)代入y=![]() 得:k=-8,
得:k=-8,
∴反比例函数的关系式为:y=![]() ,
,
把B(8,b)代入得:b=-1,
∴B(8,-1)
因此a=-2,b=-1;
如图,作点B关于x轴的对称点B′,直线AB′与x轴交于P,
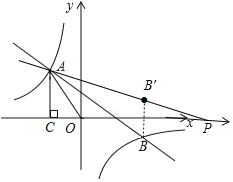
此时PA-PB最大(PA-PB=PA-PB′≤AB′,共线时差最大).
∵B(8,-1)
∴B′(8,1)
设直线AP的关系式为y=kx+b,将 A(-2,4),B′(8,1)代入得:
![]() ,
,
解得:k=![]() ,b=
,b=![]() ,
,
∴直线AP的关系式为![]() ,
,
当y=0时,即![]() =0,
=0,
解得x=![]() ,
,
∴P(![]() ,0).
,0).
故答案为:(![]() ,0).
,0).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目