题目内容
如图,在直角坐标系中,⊙P的圆心P在x轴上,⊙P与x轴交于点E、F,与y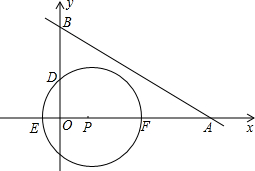 轴交于点C、D,且EO=1,CD=2
轴交于点C、D,且EO=1,CD=2| 3 |
(1)当m=3时,求经过A、B两点的直线解析式;
(2)当B点在y轴上运动时,若直线AB与⊙P保持相交,求m的取值范围.
分析:(1)把(0,3)、(5,0)分别代入y=kx+b,得到方程组,求解即可得到经过A、B两点的直线解析式;
(2)假设当B点移到B'时,直线AB'与⊙P相切于点H,连接PH、PD,由EO=1,CD=2
,可求得半径长为2,从而得出PH=2,AP=4,所以∠EAH=30°;由正切值可求出OB',要使直线AB'与⊙P相交,使m的值小于OB'的值即可;同理求出OB''的值,使m的值大于OB''即可.
(2)假设当B点移到B'时,直线AB'与⊙P相切于点H,连接PH、PD,由EO=1,CD=2
| 3 |
解答:解:(1)当m=3时,B的坐标为(0,3).
设经过A、B两点的直线解析式为y=kx+b,由题意得
,
解得
,
∴经过A、B两点的直线解析式为y=-
x+3;
(2)假设当B点移到B'时,直线AB'与⊙P相切于点H,连接PH、PD,设圆的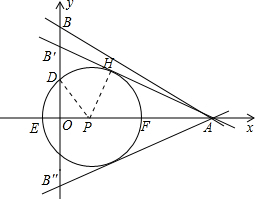 半径为x,
半径为x,
∵EO=1,CD=2
,
∴PD2=OD2+OP2,
即x2=(
)2+(x-1)2,解得x=2;
∵OA=5,
∴AP=OA-OP=5-1=4,
在Rt△APH中,PH=2,AP=4,
∴∠PAH=30°,
在Rt△AEB'中,OB'=tan30°×5=
;
同理OB''=-
,
∴若直线AB与⊙P保持相交,m的取值范围是-
<m<
.
设经过A、B两点的直线解析式为y=kx+b,由题意得
|
解得
|
∴经过A、B两点的直线解析式为y=-
| 3 |
| 5 |
(2)假设当B点移到B'时,直线AB'与⊙P相切于点H,连接PH、PD,设圆的
 半径为x,
半径为x,∵EO=1,CD=2
| 3 |
∴PD2=OD2+OP2,
即x2=(
| 3 |
∵OA=5,
∴AP=OA-OP=5-1=4,
在Rt△APH中,PH=2,AP=4,
∴∠PAH=30°,
在Rt△AEB'中,OB'=tan30°×5=
| 5 |
| 3 |
| 3 |
同理OB''=-
| 5 |
| 3 |
| 3 |
∴若直线AB与⊙P保持相交,m的取值范围是-
| 5 |
| 3 |
| 3 |
| 5 |
| 3 |
| 3 |
点评:此类题目是函数与圆的知识的综合运用,难点在第(2)题,解决的根据是直线和圆相交?圆心到直线的距离小于圆的半径.

练习册系列答案
相关题目

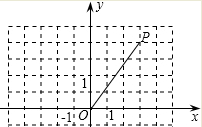 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
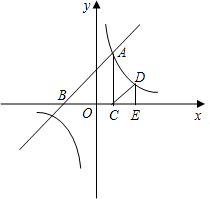
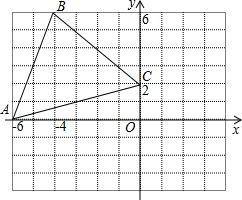 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: