Question

【题目】如图，四边形中，，，，设的长为，四边形的面积为，则与之间的函数关系式是________．

Answer 1

【答案】

【解析】

作DF⊥AC垂足为F点，易证△ABC≌△ADF，根据全等三角形的性质可得BC=AF，AC=DF，设BC=AF =a，则DF= AC=4BC=4a，CF=AC-AF =3a，在Rt△CDF中，由勾股定理求得a=，根据y=S△ABC+S△ACD即可求得与之间的函数关系式.

作DF⊥AC垂足为F点，∴∠AFD=90°，

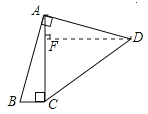
∵∠BAD=∠AFD =90°，即∠BAC+∠CAD=∠CAD+∠ADF,

∴∠BAC=∠ADF，

又∵AB=AD，∠ACB=∠AFD=90°

∴△ABC≌△ADF（AAS）

∴BC=AF，AC=DF，

设BC=AF =a，则DF= AC=4BC=4a，

CF=AC-AF =3a，

在Rt△CDF中，由勾股定理得，

CF2+DF2=CD2，即（3a）2+（4a）2=x2，

解得：a=，

∴y=S△ABC+S△ACD=BC·AC+DF·AC=．

故答案为：．