Question

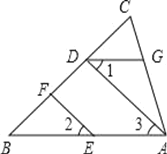
【题目】如图，△ABC中，∠ACB=90°，AB=5cm，BC=3cm，若点P从点A出发，以每秒2cm的速度沿折线A-C-B-A运动，设运动时间为t秒（t＞0）．

（1）若点P在AC上，且满足PA=PB时，求出此时t的值；

（2）若点P恰好在∠BAC的角平分线上，求t的值；

（3）在运动过程中，直接写出当t为何值时，△BCP为等腰三角形．

Answer 1

【答案】（1）；（2）；（4），5，，.

【解析】

试题（1）设存在点P，使得PA=PB，此时PA=PB=2t，PC=4-2t，根据勾股定理列方程即可得到结论；

（2）当点P在∠CAB的平分线上时，如图1，过点P作PE⊥AB于点E，此时BP=7-2t，PE=PC=2t-4，BE=5-4=1，根据勾股定理列方程即可得到结论；

（3）在Rt△ABC中，根据勾股定理得到AC=4cm，根据题意得：AP=2t，当P在AC上时，△BCP为等腰三角形，得到PC=BC，即4-2t=3，求得t=，当P在AB上时，△BCP为等腰三角形，若CP=PB，点P在BC的垂直平分线上，如图2，过P作PE⊥BC于E，求得t=，若PB=BC，即2t-3-4=3，解得t=5，③PC=BC，如图3，过C作CF⊥AB于F，由射影定理得；BC2=BFAB，列方程32=×5，即可得到结论．

试题解析：（1）设存在点P，使得PA=PB，

此时PA=PB=2t，PC=4-2t，

在Rt△PCB中，PC2+CB2=PB2，

即：（4-2t）2+32=（2t）2，

解得：t=，

∴当t=时，PA=PB；

（2）当点P在∠CAB的平分线上时，如图1，过点P作PE⊥AB于点E，

此时BP=7-2t，PE=PC=2t-4，BE=5-4=1，

在Rt△BEP中，PE2+BE2=BP2，

即：（2t-4）2+12=（7-2t）2，

解得：t=，

∴当t=时，P在△ABC的角平分线上；

（3）在Rt△ABC中，∵AB=5cm，BC=3cm，

∴AC=4cm，

根据题意得：AP=2t，

当P在AC上时，△BCP为等腰三角形，

∴PC=BC，即4-2t=3，

∴t=，

当P在AB上时，△BCP为等腰三角形，

①CP=PB，点P在BC的垂直平分线上，

如图2，过P作PE⊥BC于E，

∴BE=BC=，

∴PB=AB，即2t-3-4=，解得：t=，

②PB=BC，即2t-3-4=3，

解得：t=5，

③PC=BC，如图3，过C作CF⊥AB于F，

∴BF=BP，

∵∠ACB=90°，

由射影定理得；BC2=BFAB，

即33=×5，

解得：t=，

∴当t=，5，，时，△BCP为等腰三角形．