题目内容
 已知如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB,交CB的延长线于G,连接GF,若AD⊥BD.下列结论:
已知如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB,交CB的延长线于G,连接GF,若AD⊥BD.下列结论:①DE∥BF;②四边形BEDF是菱形;③FG⊥AB;④S△BFG=
| 1 | 4 |
其中正确的是
分析:①根据题意可证明四边形DEBF为平行四边形,继而可判断出此项正确;
②根据①的结论,再结合AD⊥BD,E为边AB的中点得出DE=BE=AE可判断出四边形BEDF是菱形.
③要使FG⊥AB,则BF=BC=BG,而因为得不出BF=BC,即不等得出FG⊥AB.
④S△BFG=
S△FCG,S△FCG=
S平行四边形ABCD,可得出结论.
②根据①的结论,再结合AD⊥BD,E为边AB的中点得出DE=BE=AE可判断出四边形BEDF是菱形.
③要使FG⊥AB,则BF=BC=BG,而因为得不出BF=BC,即不等得出FG⊥AB.
④S△BFG=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:①∵在平行四边形ABCD中,E、F分别为边AB、CD的中点
∴四边形DEBF为平行四边形,
∴DE∥BF故①正确.
②由①知四边形DEBF为平行四边形,
∵AD⊥BD,E为边AB的中点,
∴DE=BE=AE,
∴四边形BEDF是菱形故②正确.
③∵AG∥DB AD∥BG AD⊥BD
∴AGBD为矩形,
∴AD=BG=BC,
要使FG⊥AB,则BF=BC=BG,
不能证明BF=BC,即FG⊥AB不恒成立,
故③不正确.
④由③知BC=BG
∴S△BFG=
S△FCG,
∵F为CD中点
∴S△FCG=
S平行四边形ABCD
∴S△BFG=
S平行四边形ABCD
故④正确.
综上可得:①②④正确.
故答案为:①②④.
∴四边形DEBF为平行四边形,
∴DE∥BF故①正确.
②由①知四边形DEBF为平行四边形,
∵AD⊥BD,E为边AB的中点,
∴DE=BE=AE,
∴四边形BEDF是菱形故②正确.
③∵AG∥DB AD∥BG AD⊥BD
∴AGBD为矩形,
∴AD=BG=BC,
要使FG⊥AB,则BF=BC=BG,
不能证明BF=BC,即FG⊥AB不恒成立,
故③不正确.
④由③知BC=BG
∴S△BFG=
| 1 |
| 2 |
∵F为CD中点
∴S△FCG=
| 1 |
| 2 |
∴S△BFG=
| 1 |
| 4 |
故④正确.
综上可得:①②④正确.
故答案为:①②④.
点评:本题考查平行四边形的性质、菱形的性质及判定,还有全等三角形的知识,综合性较强,解答此类题目时要注意由结论推条件,把结论当做已知条件求解.

练习册系列答案
相关题目

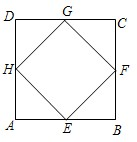 四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.
四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.

