题目内容
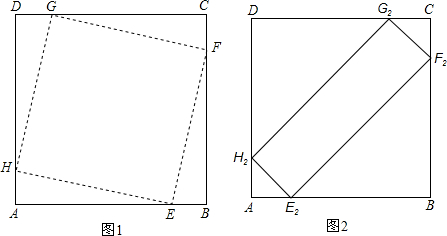
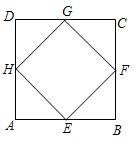
 四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.
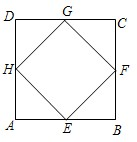
四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.(1)若点E、F、G、H是正方形ABCD四边中点,试求四边形EFGH的面积;
(2)设AE=x,AH=y,请探讨当x、y满足什么条件时,四边形EFGH是矩形.(要求写出过程)
分析:(1)直接利用相似多边形的性质,可知面积比等于相似比的平方可求得S□EFGH=2;
(2)四边形EFGH是正方形ABCD的内接平行四边形,要成为矩形的前提是四边形EFGH必须是平行四边形,则根据平行四边形的性质可求得:△AEH≌△CGF,△AEH∽△BFE,所以根据成比例线段的关系可得到
=
,化简即可得到x=y或x+y=4,即当x、y满足x=y或x+y=4时,四边形EFGH是矩形.
(2)四边形EFGH是正方形ABCD的内接平行四边形,要成为矩形的前提是四边形EFGH必须是平行四边形,则根据平行四边形的性质可求得:△AEH≌△CGF,△AEH∽△BFE,所以根据成比例线段的关系可得到
| y |
| x |
| 4-x |
| 4-y |
解答:解:(1)∵点E、F、G、H是正方形ABCD四边中点,
∴□ABCD∽□EFGH,
∴S□ABCD:S□EFGH=BC2:EF2=2:1,
∴S□EFGH=2;
(2)由题意可知△AEH≌△CGF,
∴CF=AH=y,
∵△AEH∽△BFE,
∴
=
即
=
,
化简得:(x-y)(x+y-4)=0,
∴x=y或x+y=4,
∴当x、y满足x=y或x+y=4时,四边形EFGH是矩形.
∴□ABCD∽□EFGH,
∴S□ABCD:S□EFGH=BC2:EF2=2:1,
∴S□EFGH=2;
(2)由题意可知△AEH≌△CGF,
∴CF=AH=y,
∵△AEH∽△BFE,
∴
| AH |
| AE |
| BE |
| BF |
| y |
| x |
| 4-x |
| 4-y |
化简得:(x-y)(x+y-4)=0,
∴x=y或x+y=4,
∴当x、y满足x=y或x+y=4时,四边形EFGH是矩形.
点评:主要考查了正方形的性质,相似三角形的判定及中位线的定理的综合运用.

练习册系列答案
相关题目