题目内容
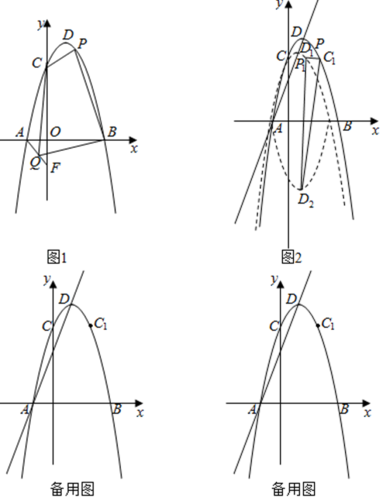
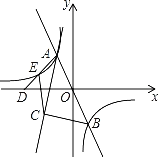
【题目】如图,过原点的直线y1=mx(m≠0)与反比例函数y2=![]() (k<0)的图象交于A、B两点,点A在第二象限,且点A的横坐标为﹣1,点D在x轴负半轴上,连接AD交反比例函数图象于另一点E,AC为∠BAD的平分线,过点B作AC的垂线,垂足为C,连接CE,若AD=2DE,△AEC的面积为
(k<0)的图象交于A、B两点,点A在第二象限,且点A的横坐标为﹣1,点D在x轴负半轴上,连接AD交反比例函数图象于另一点E,AC为∠BAD的平分线,过点B作AC的垂线,垂足为C,连接CE,若AD=2DE,△AEC的面积为![]() .
.
(1)根据图象回答:当x取何值时,y1<y2;
(2)求△AOD的面积;
(3)若点P的坐标为(m,k),在y轴的轴上是否存在一点M,使得△OMP是直角三角形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)﹣1<x<0或x>1;(2)3;(3)存在,点M的坐标为(0.﹣2)或(0,﹣4).
【解析】
(1)根据题意得到点A,点B关于原点对称,求得点B的横坐标为1,于是得到当x取﹣1<x<0或x>1时,y1<y2;
(2)连接OC,OE,求得OA=OB,得到∠OAC=∠OCA,根据角平分线的定义得到∠OAC=∠DAC,推出AD//OC,得到![]() ,即可得到答案;
,即可得到答案;
(3)作EF⊥x轴于F,AH⊥x轴于H,则EF//AH,求得DF=FH,根据三角形中位线定理得到EF=![]() AH,求得y=﹣
AH,求得y=﹣![]() ,得到A(﹣1,2),于是得到P(﹣2,﹣2),根据直角三角形的性质即可得到结论.
,得到A(﹣1,2),于是得到P(﹣2,﹣2),根据直角三角形的性质即可得到结论.
解:(1)∵直线![]() =mx(m≠0)与反比例函数
=mx(m≠0)与反比例函数![]() (k<0)的图象交于A、B两点,且点A的横坐标为﹣1,
(k<0)的图象交于A、B两点,且点A的横坐标为﹣1,
∴点A,点B关于原点对称,
∴点B的横坐标为1,
∴当x取﹣1<x<0或x>1时,y1<y2;
(2)连接OC,OE,
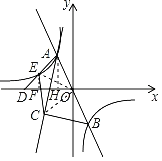
由图象知,点A,点B关于原点对称,
∴OA=OB,
∵AC⊥CB,
∴∠ACB=90°,
∴OC=![]() AB=AO,
AB=AO,
∴∠OAC=∠OCA,
∵AC为∠BAD的平分线,
∴∠OAC=∠DAC,
∴∠OCA=∠DAC,
∴AD//OC,
∴![]() ,
,
∵AD=2DE,
∴AE=DE,
∴![]() ;
;
(3)作EF⊥x轴于F,作AH⊥x轴于H,如上图,
则EF//AH,
∵AD=2DE,
∴DE=EA,
∵EF//AH,
∴![]() ,
,
∴DF=FH,
∴EF是△DHA的中位线,
∴EF=![]() AH,
AH,
∵![]()
∴OFEF=OHHA,
∴OH=![]() OF,
OF,
∴OH=HF,
∴DF=FH=HO=![]() DO,
DO,
∴![]() ,
,
∴![]() ,
,
∴k=﹣2,
∴y=![]() ,
,
∵点A在y=![]() 的图象上,
的图象上,
∴把x=﹣1代入得,y=2,
∴A(﹣1,2),
∵点A在直线y=mx上,
∴m=﹣2,
∴P(﹣2,﹣2),
在y轴上找到一点M,使得△OMP是直角三角形,
当∠OMP=90°时,PM⊥y轴,
则OM=2,
∴点M的坐标为(0.﹣2);
当∠OPM=90°时,过P作PG⊥y轴于G,则△OPM是等腰直角三角形,
∴OM=2PG=4,
∴点M的坐标为(0.﹣4);
综上所述,点M的坐标为(0.﹣2)或(0,﹣4).

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案