题目内容
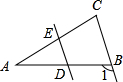 如图,已知DE∥BC,∠1=105°,∠AED=65°,则∠A的度数等于
如图,已知DE∥BC,∠1=105°,∠AED=65°,则∠A的度数等于
- A.50°
- B.40°
- C.30°
- D.60°
B
分析:先根据两直线平行,同位角相等求出∠1的同位角的度数,然后在△ADE中,根据三角形的一个外角等于与它不相邻的两个内角的和即可解答.
解答: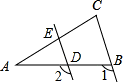 解:如图所示,∵DE∥BC,∠1=105°,
解:如图所示,∵DE∥BC,∠1=105°,
∴∠2=∠1=105°,
在△ADE中,∵∠AED=65°,
∴∠A=∠2-∠AED=105°-65°=40°.
故选B.
点评:本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键.
分析:先根据两直线平行,同位角相等求出∠1的同位角的度数,然后在△ADE中,根据三角形的一个外角等于与它不相邻的两个内角的和即可解答.
解答:
 解:如图所示,∵DE∥BC,∠1=105°,
解:如图所示,∵DE∥BC,∠1=105°,∴∠2=∠1=105°,
在△ADE中,∵∠AED=65°,
∴∠A=∠2-∠AED=105°-65°=40°.
故选B.
点评:本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
 16、如图,已知DE∥BC,AB∥CD,E为AB的中点,∠A=∠B.下列结论:
16、如图,已知DE∥BC,AB∥CD,E为AB的中点,∠A=∠B.下列结论: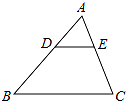 如图,已知DE∥BC,AD=2,BD=3,AE=1,那么AC的长是
如图,已知DE∥BC,AD=2,BD=3,AE=1,那么AC的长是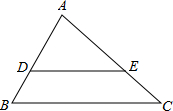 如图,已知DE∥BC,
如图,已知DE∥BC,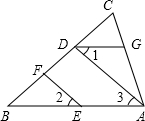 (1)如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整.
(1)如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整.