题目内容
 (1)如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整.
(1)如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整.∵EF∥AD,
已知
已知
∴∠2=
∠3
∠3
.两直线平行,同位角相等
两直线平行,同位角相等
又∵∠1=∠2,
已知
已知
∴∠1=∠3.
等量代换
等量代换
∴AB∥
DG
DG
.内错角相等,两直线平行
内错角相等,两直线平行
∴∠BAC+
∠AGD
∠AGD
=180°.两直线平行,同旁内角互补
两直线平行,同旁内角互补
又∵∠BAC=70°,
已知
已知
∴∠AGD=
110°
110°
.数据计算
数据计算

(2)如图,已知DE∥BC,∠B=80°,∠C=56°,求∠ADE和∠DEC的度数.
(3)一个多边形的每一个外角都等于24°,求这个多边形的边数.
(4)判断下列命题是真命题还是假命题,如果是真命题,指出命题的题设和结论;如果是假命题举出一个反例
①相等的角是对顶角; ②两直线平行,内错角相等.
分析:(1)根据平行线的性质与判定对各步骤进行完善;
(2)根据两直线平行,同位角相等求出∠ADE,根据两直线平行,同旁内角互补求出∠DEC;
(3)根据正多边形的边数=360°÷每一个外角的度数,进行计算即可得解;
(4)根据命题的定义对两个小题进行判定.
(2)根据两直线平行,同位角相等求出∠ADE,根据两直线平行,同旁内角互补求出∠DEC;
(3)根据正多边形的边数=360°÷每一个外角的度数,进行计算即可得解;
(4)根据命题的定义对两个小题进行判定.
解答:解:(1)∵EF∥AD,(已知)
∴∠2=∠3.(两直线平行,同位角相等)
又∵∠1=∠2,(已知)
∴∠1=∠3.(等量代换)
∴AB∥DG.(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°.(两直线平行,同旁内角互补)
又∵∠BAC=70°,(已知)
∴∠AGD=110°.(数据计算)
(2)∵DE∥BC,∠B=80°,∠C=56°,
∴∠ADE=∠B=80°,∠DEC=180°-∠C=180°-56°=124°;
(3)∵多边形的每一个外角都等于24°,
∴这个多边形的边数=360°÷24°=15;
(4)①相等的角是对顶角是假命题,例如:角平分线分成的两个角相等,但不是对顶角;
②两直线平行,内错角相等是真命题,题设是:两条直线是平行线,结论是:内错角相等.
∴∠2=∠3.(两直线平行,同位角相等)
又∵∠1=∠2,(已知)
∴∠1=∠3.(等量代换)
∴AB∥DG.(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°.(两直线平行,同旁内角互补)
又∵∠BAC=70°,(已知)
∴∠AGD=110°.(数据计算)
(2)∵DE∥BC,∠B=80°,∠C=56°,
∴∠ADE=∠B=80°,∠DEC=180°-∠C=180°-56°=124°;
(3)∵多边形的每一个外角都等于24°,
∴这个多边形的边数=360°÷24°=15;
(4)①相等的角是对顶角是假命题,例如:角平分线分成的两个角相等,但不是对顶角;
②两直线平行,内错角相等是真命题,题设是:两条直线是平行线,结论是:内错角相等.
点评:本题考查了平行线的性质与判定,多边形的内角与外角,真假命题的判断,与命题的定义,是基础题,比较简单,熟练掌握概念与性质是解题的关键.

练习册系列答案
相关题目
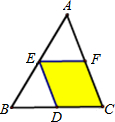 16、如图,EF是△ABC的中位线,将△AEF沿AB方向平移到△EBD的位置,点D在BC上,已知△AEF的面积为5,则图中阴影部分的面积为
16、如图,EF是△ABC的中位线,将△AEF沿AB方向平移到△EBD的位置,点D在BC上,已知△AEF的面积为5,则图中阴影部分的面积为 3、如图,EF为梯形ABCD的中位线,AH平分∠DAB交EF于M,延长DM交AB于N.
3、如图,EF为梯形ABCD的中位线,AH平分∠DAB交EF于M,延长DM交AB于N.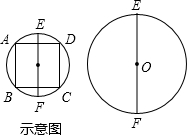 (1)如图,EF是⊙O的直径,请仅用尺规作出该圆的内接正方形ABCD,要求所作正方形的一组对边AD、BC垂直于EF.(见示意图;不写作法,但须保留作图痕迹);
(1)如图,EF是⊙O的直径,请仅用尺规作出该圆的内接正方形ABCD,要求所作正方形的一组对边AD、BC垂直于EF.(见示意图;不写作法,但须保留作图痕迹);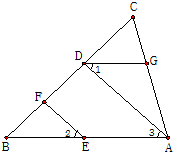 24、如图,EF∥AD,∠1=∠2,∠BAC=65°.将下面求∠AGD的过程填写完整.
24、如图,EF∥AD,∠1=∠2,∠BAC=65°.将下面求∠AGD的过程填写完整.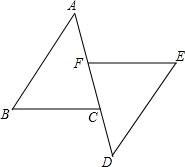 已知:如图,EF∥BC,点F,点C在AD上,BC=EF,AC=DF.
已知:如图,EF∥BC,点F,点C在AD上,BC=EF,AC=DF.